Services
How to cite this paperAn. 3. Enc. Energ. Meio Rural 2003
Otimização exergética de sistemas de refrigeração por absorção através da SRM
Joel Carlos Zukowski JrI; Luís Augusto Barbosa CortezII
IFaculdade de Engenharia Agrícola.Centro Universitário Luterano de Palmas. TO., CEP 77000-000 Palmas, TO tel: (063) 223-2055 fax: (063) 223-2091
IIDepartamento de Construções Rurais, Faculdade de Engenharia Agrícola da UNICAMP., CEP Campinas, SP tel: (019) 788-1033 fax: (019) 788-1010
RESUMO
Devido à carência de energia elétrica nas propriedades rurais, alternativas para a conservação de produtos agropecuários devem ser adotadas. A refrigeração por absorção pode ser uma solução economicamente viável. Estes sistemas consomem pouca ou nenhuma energia elétrica, mas necessitam de energia térmica. Para garantir o menor consumo de energia, ou seja, a melhor relação custo-benefício, é necessário a análise dos parâmetros que mais influenciam a eficiência exergética. Esta determinação pode determinar a melhor condição de operação ou uma faixa de valores que propiciam obter o maior benefício desejado. Este trabalho apresenta uma aplicação de SRM (Surface Response Method) na determinação, dentre os parâmetros estudados, quais mais influenciam a eficiência exergética de um sistema de refrigeração por absorção água-amônia para produção de gelo. Tal determinação propicia a otimização experimental deste tipo de sistema. Mostra também que a SRM é uma ferramenta poderosa na otimização deste tipo de sistema.
Palavras-chave: exergia, eficiência exergética, refrigeração por absorção, água-amônia, SRM.
ABSTRACT
Due to electric energy deficit in the rural properties, alternatives for the conservation of agricultural products should be adopted. The absorption refrigeration can be economically a viable solution. These systems consume little or no electric energy, but they need thermal energy instead. In order to guarantee the best cost-benefit relationship, is necessary to conduct the analysis of the parameters that influence the most the exergetic efficiency. This determination can define the best operation condition or a range of values that allow to obtain the maximum benefit. This work presents an application of SRM (Surface Response Method) in the determination, among the studied parameters, which most influence the exergetic efficiency of water-ammonia refrigeration absorption system for ice production. Such determination allows the experimental optimization and also shows that SRM is a powerful tool in the optimization for this type of system.
INTRODUÇÃO
Um dos fatores para o desenvolvimento das propriedades rurais é a oferta de energia elétrica. No Brasil a oferta de energia elétrica nas propriedades rurais varia de acordo com a região. Nas regiões sul e sudeste mais de 50% das propriedades rurais têm energia elétrica disponível, no entanto nas regiões norte, Centro-Oeste e nordeste menos de 10% das propriedades rurais estão servidas de tal fonte de energia.
A falta de energia elétrica inviabiliza a utilização de sistemas de refrigeração na aplicação de tratamento pós-colheita frigorificado que devem ser utilizados principalmente para frutas e hortaliças, produtos agrícolas que, atualmente, apresentam maior porcentagem de perdas (até 30% antes de chegar nos postos de venda a varejo).
Sob o ponto de vista energético, em certos cenários a utilização de sistemas de refrigeração por absorção pode ser mais interessante que a utilização de sistemas de refrigeração por compressão. As propriedades rurais brasileiras, bem como de outros países em desenvolvimento, em sua maioria não são providas de energia elétrica e os sistemas de refrigeração por absorção, não são grandes consumidores desta fonte de energia
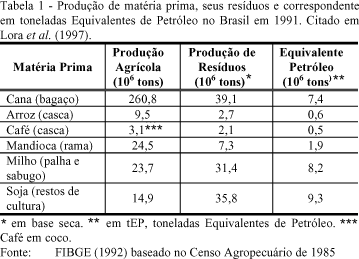
Dentre as fontes de energia possíveis de serem utilizadas está a biomassa formada por resíduos da produção agrícola. Por ser um grande produtor agrícola, há no Brasil uma grande disponibilidade de biomassa para produção de energia. Cortez & Lora (1997) fazem um estudo neste sentido. A tabela 1 mostra uma estimativa da produção agrícola e da geração de resíduos de algumas culturas que podem ser utilizados como fonte de energia seja para queima direta ou para geração de biogás. Martins (1989), apresentou um estudo sobre a utilização de fogão a lenha em conjunto com sistema de refrigeração por absorção de porte doméstico.
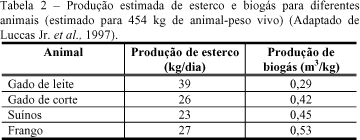
Além dos resíduos vegetais, encontra-se, nas propriedades rurais, uma grande quantidade de resíduos animais que podem ser utilizados para produção de biogás ( Lora et al. 1997). A tabela 2 mostra uma estimativa da produção de esterco e de biogás para alguns tipos de animais.
A energia térmica necessária em sistemas de refrigeração por absorção pode ser obtida através da queima direta do biogás como fonte de calor ou da utilização em sistemas de cogeração, onde o biogás é utilizado como combustível para grupos geradores, motor de combustão interna-gerador de eletricidade, aproveitando-se o calor dos gases de escape como fonte de calor necessário para sistema de refrigeração por absorção, tanto para porte doméstico como sistemas de maior porte.
Nas regiões Norte e Nordeste do Brasil onde a necessidade de refrigeração para conservação da produção agrícola, principalmente de frutas e hortaliças, é mais evidente, a utilização de sistemas de refrigeração por absorção é uma alternativa a ser considerada. A utilização da energia solar como fonte de calor e para geração de energia elétrica é uma alternativa para a carência de energia elétrica nestas regiões e, portanto, uma forma de se viabilizar a utilização de sistemas de refrigeração por absorção, tanto para condicionamento de ar, como para tratamento pós-colheita e industrialização de produtos agrícolas.
Onde houver energia térmica disponível e de baixo custo, seja ela advinda da queima direta da biomassa, de biogás, de gases de escape de motores a combustão interna, solar ou de vapor residual de processos, a tecnologia de refrigeração por absorção pode ser empregada.
Para garantir um melhor aproveitamento da energia térmica e elétrica disponível é necessário aumentar a eficiência dos sistemas de refrigeração por absorção. Este trabalho apresenta um método estatístico para otimização da eficiência exergética, que consiste na aplicação de planejamento experimental fatorial de dois níveis associado com o método de análise da superfície de resposta (Surface Response Method -SRM).
Este método foi utilizado para determinar quais dos parâmetros de operação do sistema de refrigeração por absorção água-amônia, instalado no HC-UNICAMP, mais influenciam a eficiência exergética, bem como as interações entre eles. Após verificar a resposta do sistema à variação dos parâmetros, obteve-se uma função objetivo relacionando a eficiência exergética com os parâmetros estatisticamente mais significativos, que possibilitou a otimização do sistema, afim de se determinar o maior rendimento possível com o menor consumo de energia (térmica e/ou elétrica) para o sistema em estudo.
Os resultados obtidos mostram que esta metodologia é propícia para otimizar sistemas de refrigeração por absorção
METODOLOGIA DE OTIMIZAÇÃO DE SISTEMAS DE REFRIGERAÇÃO POR ABSORÇÃO.
AVALIAÇÃO TERMODINÂMICA DO SISTEMA DE REFRIGERAÇÃO POR ABSORÇÃO
A avaliação termodinâmica de primeira lei, (ASHRAE, 1997), é importante para estudos sobre novos pares refrigerantes, melhoramentos nos ciclos, avaliação dos efeitos da variação das condições de operação etc. O uso da segunda lei é descrito como a forma para se obter a quantificação das irreversibilidades em cada componente do sistema.
A ASHRAE (1997) ainda não apresenta metodologia de avaliação termodinâmica de segunda lei para sistemas de absorção, citando apenas esta metodologia para sistemas de compressão. Contudo a bibliografia citada é profícua nesta metodologia.
A avaliação exergética dos ciclos de absorção já era utilizada por Altenkirch e Nierbergall no início do século, apesar de não ser denominada assim, quando grande parte do desenvolvimento teórico desta tecnologia foi feita. Koshkin (1968) explica que o coeficiente de desempenho (COP) não mostra o desempenho termodinâmico de todos os processos envolvidos, não revela as perdas exergéticas e as causas que as determinam em cada equipamento. Aphornratana (1995) mostra que pela primeira lei, o ciclo total da transferência de calor é igual ao da transferência de trabalho. Como a primeira lei não distingue calor e trabalho, não pode mostrar quanto de trabalho pode ser ou não convertido em calor e vice-versa. Segundo ela, todas as formas de energia podem ser convertidas umas nas outras. No entanto, a segunda lei da termodinâmica define limites para a conversão de energia. Por exemplo: trabalho pode ser totalmente transformado em calor mas não é possível transformar calor totalmente em trabalho.
Van Wylen (1995) mostra alguns fatores que causam irreversibilidades nos processos:
1. Atrito mecânico: trabalho é transformado em calor.
2. Transferência de calor entre dois corpos a temperaturas diferentes: Quanto maior o diferencial de temperatura, maior a irreversibilidade. Este processo não pode ser revertido sem trabalho externo.
3. Expansão não resistida e queda de pressão: Podem ser processos aproximadamente adiabáticos, mas irreversíveis. A pressão não pode aumentar sem trabalho externo.
4. Mistura de substâncias diferentes inicialmente separados: Não é possível separá-las sem transferência de calor.
A metodologia exergética por sua vez leva em conta não somente as quantidades de calor transferido, como também o potencial de temperatura que determina a capacidade de realização de trabalho de cada fluxo.
A metodologia para o cálculo dos fluxos de exergia e as variações de exergia (ou irreversibilidades) de cada componente é descrito por Szargut (1988). Ataer & 
(1991) fazem um estudo comparativo das irreversibilidades nos sistemas de refrigeração por absorção. Cortez et al. (1997), apresentam uma avaliação exergética do sistema de absorção para produção de gelo instalado na UNICAMP, 
(1988), apresenta um estudo das irreversibilidades em uma planta por absorção brometo de lítio-água e água-amônia mostrando que nos sistemas por ele estudados o sistema com o par brometo de lítio-água apresentou menores irreversibilidades. Oliveira Jr. (1992) faz uma análise dos processos de separação e de mistura dos fluidos usados em sistemas por absorção. Porneala & Porneala (1993) apresentam uma metodologia de cálculo e otimização de sistemas por absorção usando a abordagem exergética. Para simplificar os cálculos, eles utilizaram sistemas de equações lineares. Os parâmetros para otimização por eles utilizados foram a pressão de evaporação e a concentração da solução da solução intermediária em uma planta usando o par brometo de lítio-água. Neste trabalho eles fazem uma comparação entre os sistemas de refrigeração por absorção e por compressão usando amônia e R12, respectivamente. Para os sistemas de compressão estudados o parâmetro analisado foi a pressão de evaporação. A função objetivo foi a eficiência exergética como função desta pressão. Também Kotas (1985) descreve detalhadamente as irreversibilidades associadas aos processos de separação, mistura, trocas de calor e expansão. Jordan (1985) descreve detalhadamente uma metodologia para avaliação exergética de um ciclo de absorção, embora, ainda não publicada pelo autor.
CÁLCULO DA EFICIÊNCIA DO CICLO DE ABSORÇÃO
Para uma avaliação de segunda lei pode-se empregar a equação descrita por Szargut (1988). Adotando-se o sinal positivo para o calor que é transferido ao fluído de trabalho no gerador, pode-se escrever a seguinte equação:
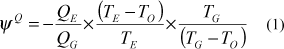
A equação acima calcula a exergia transferida no gerador e no evaporador a partir da quantidade de calor transferida em cada um destes equipamentos supondo que o processo ocorra sob temperaturas constantes de TG, TE e TO. No processo real a transferência de calor se dá com a variação da temperatura, perda de carga etc. Desta forma pode-se calcular diretamente a eficiência de segunda lei do ciclo a partir dos fluxos de exergia do fluído refrigerado e do meio de aquecimento. Kotas (1988) define esta relação entre a exergia útil e a exergia que entra no sistema de eficiência racional:
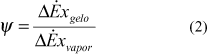
Pode-se considerar também para cálculo da eficiência exergética os fluxos de exergia referentes ao trabalho realizado pela bomba de solução e outros equipamentos acessórios (ventilador e bomba d'água do condensador evaporativo (CE) e a bomba d'água do gerador de gelo). Assim a equação (2) pode ser reescrita:
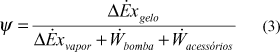
PLANEJAMENTO EXPERIMENTAL FATORIAL DE DOIS NÍVEIS
A essência de um bom planejamento consiste em projetar um experimento de forma que ele seja capaz de fornecer o tipo de informação que se procura. Para isso é preciso saber o que é que se está procurando. Pode-se dizer que um bom experimentador é, antes de tudo, uma pessoa que sabe o que quer. Dependendo do que ele queira, algumas técnicas são mais vantajosas que outras, enquanto determinadas técnicas são simplesmente inócuas (Barros Neto et al., 1995).
O progresso de uma boa atividade de investigação experimental deve evoluir, segundo Barros Neto, et al. (1995) de uma triagem de variáveis a um modelo baseado em princípios gerais, que valha para qualquer sistema do mesmo tipo, instalado em qualquer lugar, operando em quaisquer condições de operação dentre as condições possíveis.
Antes de se obter um modelo geral, pode-se obter uma descrição mais detalhada da relação entre as variáveis mais importantes e o parâmetro estudado obtendo-se um modelo sofisticado através do método dos mínimos quadrados. (Barros Neto et al., 1995).
Neste trabalho, conforme discutido anteriormente, o principal objetivo é otimizar o funcionamento do sistema em estudo, através da maximização do parâmetro: eficiência exergética (Y). Para tanto, uma das técnicas disponíveis é a Análise de Superfície de Resposta, descrita mais adiante.
O planejamento fatorial de dois níveis é construído de forma simples. Barros Neto et al., (1995) mostra como definir um planejamento fatorial de dois níveis.
Para garantir que o modelo a ser obtido seja preditivo e para que os dados sejam estatisticamente válidos é necessário que estes experimentos sejam executados de forma aleatória (Barros Neto et. al., 1995). Para tanto deve ser feito um sorteio da ordem em que cada experimento será executado.
OBTENÇÃO DA FUNÇÃO OBJETIVO
Para se obter a função objetivo do planejamento experimental fatorial completo apresentado acima, deve-se realizar uma análise estatística de acordo com a metodologia própria do método de planejamento experimental. Para tanto pode-se utilizar um "software" que faz os cálculos necessários apresentando os resultados na forma de gráficos e tabelas.
OTIMIZAÇÃO POR SRM
A metodologia para otimizar este modelo é conhecida pelo nome Metodologia da Superfície de Resposta (SRM) e foi introduzida por G.E.P. Box na década de 1950 (Barros neto et al., 1995). Barros Neto et al. (1995) descreve esta metodologia. Para maior compreensão da metodologia é necessário recorrer a obra deste autor, onde vários exemplos são apresentados. Neste caso, este modelo foi utilizado e os valores foram calculados pelo programa STATISTICA. Tal programa nos fornece todos os parâmetros necessários para verificação da validade estatística do modelo, margem de erros dos coeficientes, bem como subsídios para avaliar a predição da resposta em função das variáveis de interesse.
VALIDAÇÃO ESTATÍSTICA DO MODELO
Para validação estatística do modelo obtido utilizou-se a análise de variância, também conhecido como teste estatístico "F". Isto significa que os resíduos apresentam uma distribuição normal e que a razão entre as médias quadráticas da regressão e dos resíduos seguem uma distribuição "F". Para facilitar a visualização e a análise deve-se construir a tabela ANOVA (ANalyze Of VAriance).
O intervalo de confiança adotado foi de 95%, ou seja uma significância estatística de 5%.
DESCRIÇÃO DO SISTEMA EM ESTUDO
A figura 1 apresenta um esquema do sistema de refrigeração por absorção em estudo. A figura 2 mostra uma vista de frente.
As características gerais de projeto do sistema são: Capacidade de Refrigeração de 23,2kW, a temperatura de evaporação -10oC, a potência térmica utilizada é 46,4kW a 110oC. A rede elétrica instalada é de 220V – trifásico. A capacidade nominal de produção de gelo é 20kg/ciclo. A duração do ciclo de congelamento é de 10 minutos. O descongelamento, feito com vapor de amônia quente que sai da entrada do condensador, tem duração de 1 minuto e é controlado por um "timer" de fabricação COEL. A espessura do gelo desejada varia entre 5 e 6 mm.
Para obter mais detalhes construtivos e de funcionamento do sistema veja Zukowski (1999).
Os parâmetros estudados foram: vazão de água de formação de gelo, vazão de água da torre de resfriamento evaporativo, pressão do vapor de água que entra no gerador, tempo de ciclo. Outras duas variáveis a serem considerada são temperaturas de bulbo seco e úmido, mas como não puderam ser controladas não fizeram parte do modelo, foram monitoradas e analisadas.
O planejamento experimental adotado é apresentado na tabela 3.
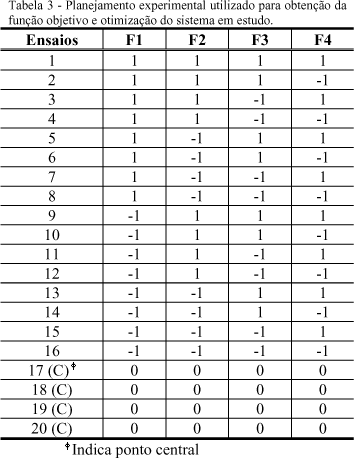
Um planejamento experimental de 4 variáveis resulta em dezesseis experimentos. Adicionando-se 4 experimentos no ponto central para determinar o erro puro perfazem um total de 20 experimentos.
Os experimentos definidos na tabela 3 foram realizados de forma aleatória e em diferentes horários do dia.
As faixas de valores de cada parâmetro estudado são definidas considerando-se as limitações físicas do equipamento, como segue:
A vazão no condensador é limitada por fatores físicos. O valor de projeto é de 8m3/h. Foram instalados tubos de PVC de 2". Esta nova instalação hidráulica na torre possibilitou maiores vazões de água. O rotâmetro instalado na linha de água pode medir, a 22oC, de 1 a 10m3/h. Atualmente é possível se definir vazões maiores que 10 m3/h, mas seria necessário substituir o rotâmetro. Este equipamento apresenta um custo relativamente alto (cerca de US$ 1200,00).
A vazão no evaporador também apresenta limitações físicas. Deseja-se que o fluxo de água escorra pelas paredes dos tubos anulares que formam o evaporador. A água é aspergida por orifícios de aproximadamente 1,5mm. Para vazões superiores a 2,0m3/h, ao bater na parede do evaporador, uma parte considerável da água aspergida será refletida e escorrerá pelas paredes externas que envolvem o evaporador não produzindo gelo.
A pressão do vapor de água no gerador apresenta limitações físicas. A primeira é a pressão máxima disponível que é de aproximadamente 6,0kgf/cm2 (589kPa), a segunda é que se a pressão do vapor for muito alta a temperatura no interior da coluna será bastante elevada e consequentemente a pressão de trabalho será também elevada. Por questão de segurança pressões acima de 16bar devem ser evitadas. Com temperaturas de saída de amônia da coluna superiores a 45oC a quantidade de água arrastada pela amônia aumenta, assim como para temperaturas muito baixas de operação da coluna (resultado de pressões muito baixas).
Com relação ao tempo de ciclo a limitação física é a espessura do gelo formado. Para tempos de formação de gelo maiores que 30min a espessura fica tão grande (acima de 10mm) que o britador não pode quebrá-lo sem comprometer a integridade dos tubos que interligam o evaporador ao separador de líquido.
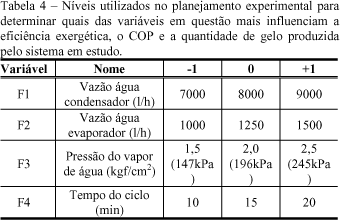
Os valores codificados, utilizados no planejamento experimental estão apresentados na tabela 4.
RESULTADOS
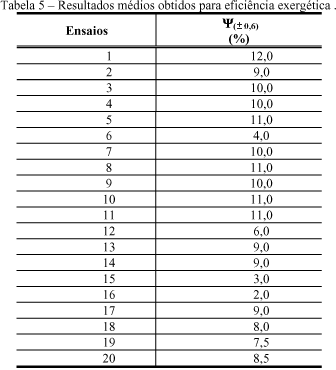
Os resultados para os experimentos está apresentado na tabela 4.
Com estes resultado, utilizando-se o programa STATISTICA, obteve-se os valores dos efeitos de cada parâmetro sobre a eficiência exergética (Y ), bem como os coeficientes do modelo proposto para otimização.
Os efeitos obtidos são: dos parâmetros individualmente, das interações entre eles de segunda, terceira e quarta ordem. Quase a totalidade dos processo reais não apresentam interações de quarta ordem. Em muitos casos as interações de terceira ordem também não estão presentes (conforme discutido anteriormente), mas para se ter certeza é necessário realizar os testes de significância estatística para estas interações.
A eficiência exergética (Y ) é a função termodinâmica que mostra de forma mais adequada quanto da energia disponível para realizar trabalho (exergia) foi transformada em trabalho e quanto dela se perdeu, sendo destruída. Neste trabalho considerou-se esta função de primordial importância na avaliação e otimização dos sistema térmico em estudo.
Assim como para os casos anteriores efetuar-se-á a análise da influência dos parâmetros em estudo na eficiência exergética (Y ). Para tanto é necessário determinar quais parâmetros realmente apresentam influência estatisticamente significativa ao nível de significância de 5%.
Na figura 3 pode-se verificar que estão presentes no modelo efeitos principais, de interação binárias e ternárias. Somente não se mostraram estatisticamente significativos os efeitos de interação entre as variáveis F1-F4, F2-F3 e F2-F4, F3-F4 e F1*F2*F4. Como estes valores não são significativos não farão parte do modelo, logo, eliminando-se os efeitos que não são estatisticamente significativos para 5% de significância, obtém-se a tabela 6 a seguir.
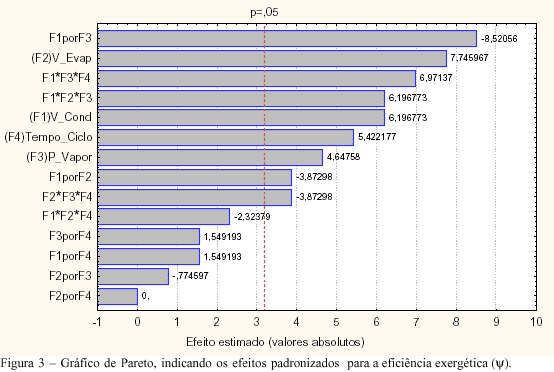
Do gráfico de Pareto (Figura 3) verifica-se que os efeitos mais importantes são a vazão no evaporador, e a interação entre a vazão no condensador e a pressão do vapor de água no gerador. As interações entre as variáveis F1*F3*F4 (Vazão de água no condensador, pressão de vapor no gerador e tempo de ciclo) mostraram-se muito importantes. Com efeitos de mesmo valor estão a vazão no condensador e as interações entre as variáveis F1*F2*F3 (Vazão de água no condensador, vazão de água no evaporador e pressão de vapor no gerador). A interação de terceira ordem F2*F3*F4 (vazão de água no evaporador, pressão de vapor no gerador e tempo de ciclo). Também mostrou-se significativa a pressão do vapor no gerador e o tempo de ciclo. Das interações de segunda ordem somente mostrou-se estatisticamente significativa a interação entre a vazão no condensador e a vazão no evaporador (F1 por F2).
A figura 4 mostra a relação entre os valores previstos e os valores ajustados. Pode se verificar que apresentam uma relação razoável, ou seja, com erros pequenos, entre os valores preditos e os observados.
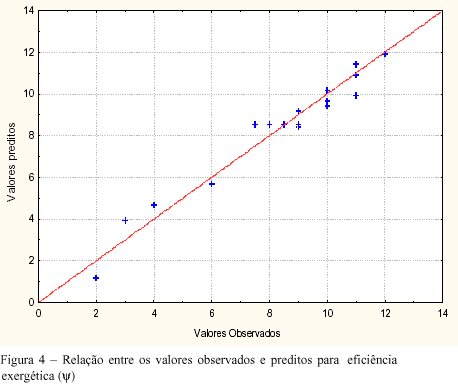
A relação entre os valores observados e preditos para a eficiência exergética mostram que o modelo ajusta bem os dados experimentais. O R2 para Y é 0,95795, ou seja R de 98%.
VALIDAÇÃO ESTATÍSTICA DO MODELO
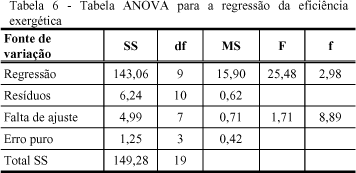
A tabela ANOVA para regressão (tabela 6) é apresentada a seguir.
Da tabela ANOVA acima (tabela 6) verifica-se que o modelo é estatisticamente significativo para o grau de significância adotado, 5%, pois o valor do fator "F" calculado para a regressão é 8,6 vezes maior que o tabelado. O Modelo ajusta-se bem aos valores experimentais pois o fator "F" calculado para a falta de ajuste é aproximadamente 5,2 vezes menor que o tabelado.
A porcentagem de variação explicada por este modelo (R2) é de 96% ou seja somente 4% dos resíduos são devido a regressão. A máxima variação explicável é de 99% ou seja, somente 0,8% dos resíduos são devido à falta de ajuste. O coeficiente de ajuste (R) é de 98%. Portanto o modelo é estatisticamente válido. A tabela 7 apresenta os coeficientes da função objetivo eficiência exergética (Y).
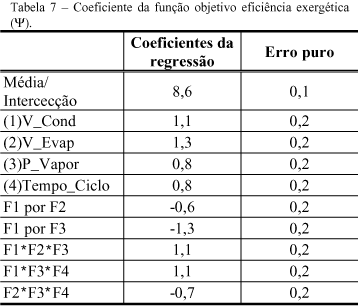
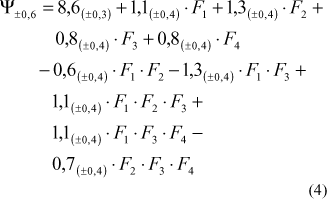
O modelo acima apresentado (equação 4) é válido somente na faixa estudada. Para se efetuar extrapolações é necessário verificar, experimentalmente, se o valor de Y obtido é válido. Para obter-se os valores de Y nesta função é necessário introduzir os valores codificados, ou seja para valores reais apresentados na tabela 4.3, deve-se calcular o nível (entre -1 e 1) correspondente e substituí-lo na equação 4.
ANÁLISE DE SUPERFÍCIE DE RESPOSTA EFICIÊNCIA EXERGÉTICA (Y )
Definido o modelo, é necessário determinar os valores que, dentro da faixa de operação estudada maximizam o valor da eficiência exergética. Para efetuar-se esta análise, assim como nos casos anteriores, utilizou-se figuras tridimensionais e de curvas de níveis que relaciona relacionando os parâmetros dois a dois, fixando os demais nos valores propostos para o planejamento.
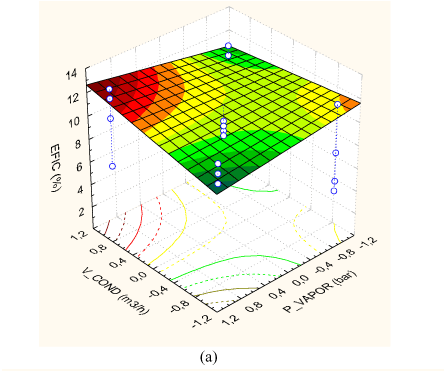
Estas figuras foram obtidas variando-se os parâmetros dentro da faixa estudada procurando se deslocar nas superfícies obtidas pelas linhas de maior crescimento da eficiência exergética. As superfícies de resposta para tal função que mostra a máxima eficiência é apresentada a seguir.
Da figura 5.a verificou-se que para valores crescentes de pressão de vapor no gerador e vazão de água no condensador a eficiência tende a subir. Verifica-se , da figura 5.b que, variando-se isoladamente cada um destes parâmetros este fato não é verdadeiro. Fica evidente que a interação entre estas duas variáveis influencia muito mais a eficiência exergética que cada uma delas em separado
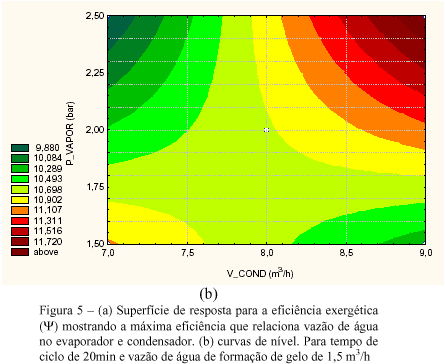
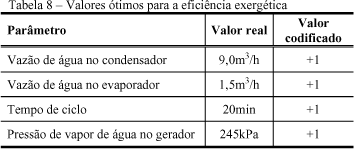
Os valores ótimos para a função objetivo são apresentados na tabela 8.
A máxima eficiência exergética é:
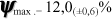
CONCLUSÕES
Do presente trabalho conclui-se que a SRM é um método apropriado para análise de sensibilidade e de otimização de sistemas térmicos.
A otimização de sistemas de refrigeração por absorção é uma tarefa árdua devido a complexidade destes sistemas. No entanto, através da metodologia estatística de planejamento experimental, efetuando-se uma análise de sensibilidade e aplicando-se a SRM pode-se otimizar a operação destes sistemas dentro de uma faixa possível e de interesse ao nível de confiança desejado. Este procedimento é muito propício para a industria devido a sua simplicidade, rapidez e eficiência. O desenvolvimento de modelos matemáticos normalmente requer muito mais tempo, comparando-se com esta metodologia. Também requer, em muitos casos, simplificações que adicionam variações entre os valores preditos pelo modelo e os valores reais obtidos experimentalmente.
A metodologia aplicada no sistema em estudo e aqui apresentada também apresenta variações, mas estas já estão previamente definidas na análise. Neste caso 5% de intervalo de confiança. Definir previamente a faixa de variação aceitável em um processo pode implicar na determinação do risco do investimento, bem como do retorno que se espera dele.
Maximizando a eficiência exergética pode-se garantir que o aproveitamento da energia total necessária para o processo está sendo utilizada da melhor maneira possível, considerando-se que não se faça alterações físicas no sistema.
A análise de segunda lei, associada ao planejamento experimental e a SRM propicia determinar, num menor tempo, quais os equipamentos do sistema apresentam maior irreversibilidades. Pode-se, a partir desta determinação, avaliar o investimento necessário para as devidas melhorias no sistema, bem como a relação custo benefício destes investimentos.
AGRADECIMENTOS
À Fundação de Amparo à Pesquisa do Estado de São Paulo – FAPESP pelo apoio financeiro, ao Centro Universitário Luterano de Palmas - CULP/ULBRA e a todos que de alguma forma contribuíram para o desenvolvimento deste trabalho.
BIBLIOGRAFIA
[1] ZUKOWSKI Jr., J.C Estudo de Sensibilidade em um Sistema de Refrigeração Por Absorção Água-Amônia. UNICAMP, 1999. [Tese de doutorado]
[2] ASHRAE - American Society of Heating, Refrigeration and Air Conditioning Engineering Fundamentals Handbook. 1997 Cap. 1, 40.
[4] APHORNRATANA, S., EAMES, I.W. Thermodynamic Analysis of Absorption Refrigeration Cycles Using the Second Law of Thermodynamics Method. Int. J. Refrig., v. 18, n. 4, p.244-252, 1995.
[5] VAN WYLEN, G, SONNTAG, R., BORGNAKKE, C. Fundamentos da termodinâmica classica. São Paulo: Edgar Blücher, 591p., 1995.
[6] SZARGUT, J. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes. Hemisphere Publishing Corporation, 1988, p 152-160.
[7] ATAER E.Ö., GÖGÜS, Y. Comparative Study of Irreversibilities in Aqua-Ammonia Absorption Refrigeration Systems. Int. Jr. Refrig., v.14, mar. 1991.
[8] CORTEZ, L.A.B., LARSON D. L., SILVA A DA,. ENERGY AND EXERGY EVALUATION OF ICE PRODUCTION BY ABSORPTION REFRIGERATION. Transactions of The ASAE, v. 40, n. 2, p. 395-403, 1997.
[9] EGIRICAN N. THE SECOND LAW ANALYSIS OF ABSORPTION COOLING CYCLES. Heat Recovery systems and CHP, v. 8, n. 6, p. 549-558, 1988
[10] Oliveria Jr., S. de, Goff, P. L., Análise Exergética dos Processos de Separação/Mistura. Aplicação aos Transformadores Térmicos com Ciclo de Absorção. In: 9o Congresso Brasileiro de Engenharia Química. Salvador, 1992, p. 567-574.
[11] Porneala, S, Porneala, D. Analysis, Calculus and Optimization Method for Thermal and Refrigerating Plants. In: Proc. Energy Systems and Ecology. Polônia, 1993, v. 2., p. 659-670.
[12] Kotas,T.J. The Exergy Method of Thermal Analysis. Great Britain. 1985, p. 29-51,99-137.
[13] Jordan, D.P.- "Exergetic evaluation of aqua-ammonia absorption refrigeration system" - Texas Tech University, 1985. [Trabalho não publicado]
[14] BARROS NETO, B. DE, SCARMINIO, I. S., BRUNS, R. E. Planejamento e Otimização de Experimentos. Campinas: UNICAMP, 1995,299 p.
