An. 4. Enc. Energ. Meio Rural 2002
Modelo Fuzzy para obtenção do tempo de aeração em silos verticais visando reduzir o consumo de energia elétrica
Fuzzy model to calculate aeration time in vertical silos to reduce electric energy consume
Luiz Francisco da CruzI; Edwin AvolioII; Nelson Miguel TeixeiraIII
IDepartamento de Matemática - FC/UNESP-Bauru/SP. Av. Eng. Luiz Edmundo Carrijo Coube, s/n - CEP: 17033-360, lfcruz@fc.unesp.br
IIDepartamento de Engenharia Elétrica - FEB/UNESP - Bauru/SP. Av. Eng. Luiz Edmundo Carrijo Coube, s/n - CEP: 17033-360, avolio@feb.unesp.br
IIIDepartamento de Engenharia Rural - FCA/UNESP - Botucatu/SP, nteixeira@fca.unesp.br
RESUMO
Este trabalho apresenta um modelo matemático, baseado na Teoria Fuzzy, para determinar o tempo de aeração de uma certa massa de grãos. Através dos procedimentos básicos de fuzzyficação, aplicação das regras fuzzy e defuzzyficação, o modelo determina o tempo de aeração necessário para que a massa de grãos atinja as condições desejadas de armazenamento (temperatura e umidade), em função das condições iniciais da massa de grãos e do ar externo (temperatura e umidade). Este tempo de aeração é tomado como tempo de referência, quando o motor de indução, que aciona o ventilador do sistema de aeração, opera com freqüência nominal igual a 60Hz. Através de um conversor de freqüência, que permite o sistema motor-ventilador operar com velocidade variável, pode-se reduzir o consumo de energia elétrica quando o motor opera com velocidade reduzida. A redução da velocidade é obtida pela conseqüente redução da freqüência através do conversor o que acarreta em um acréscimo no tempo de aeração, uma vez que a vazão total fornecida pelo ventilador também será reduzida. Portanto, o modelo permite obter a freqüência necessária, em função do acréscimo do tempo de aeração, para que o sistema opere com velocidade reduzida, visando reduzir o consumo de energia elétrica por período de aeração, sem que haja prejuízo para a massa de grãos ensilada.
Palavras-chave: Fuzzy, silo, aeração, energia elétrica.
ABSTRACT
This work presents a mathematical model based on Fuzzy Theoretical concepts to determine grain mass aeration time. Due to the fuzzyfication and defuzzyfication basic procedures which lies in its basis, the model can be considered as reliable as other ones available but, better than these, it can be used with a control system which allows us to know the electric energy consume during all over the aeration process. Considering our model working together with the technology of induction motors in a variable speed drives, we can determine an optimum operation time which takes into account not only the conservation of the grains, but also the electrical consume decreasing factor.
Keywords: Fuzzy, silo, aeration, electric energy.
INTRODUÇÃO
A aeração é a passagem forçada de ar através de uma massa de grãos armazenada em um silo, por intermédio de um ventilador, para melhorar as condições de armazenamento de grãos. O sistema de aeração é utilizado para se obter uma distribuição uniforme da movimentação do ar através da massa de grãos, de tal forma que todas as zonas das células sejam aeradas de forma homogênea, segundo Lasseran (1981).
Burrel (1973) afirma que a aeração depende, basicamente, da temperatura intergranular, da temperatura externa do ar, da umidade do grão e da umidade externa do ar. Para se avaliar a temperatura e a umidade da massa de grãos, utiliza-se uma rede de sensores, dispostos de forma regular nas células de estocagem dos silos. Estes sensores são ligados a um painel de controle que indica a temperatura e a umidade em vários níveis da massa de grãos, permitindo que o operador escolha o momento oportuno para iniciar a aeração e sua duração. Uma vez atingido os níveis adequados de temperatura e umidade o sistema é desligado, e o processo se repete sempre em função da variação destas duas grandezas.
O resfriamento da massa de grãos é um fenômeno de propagação de uma frente de esfriamento. A zona resfriada progride com a conseqüente diminuição da zona a resfriar. As trocas entre o ar e o grão se realizam numa camada de espessura limitada, chamada zona de resfriamento. A velocidade de propagação do resfriamento no grão (vg), ou seja, a velocidade de avanço da zona de resfriamento é proporcional a velocidade aparente do ar (va). Com os valores iniciais da temperatura e da umidade do ar e do grão e, com o uso do gráfico psicrométrico (Diagrama de Mollier) é possível determinar o valor da velocidade de propagação no grão.
O tempo de aeração (taer) necessário para o resfriamento completo de uma célula é diretamente proporcional a altura (H) da massa de grãos e inversamente proporcional a velocidade de propagação (vg) (Lasseran, 1981).

A velocidade de propagação da zona de resfriamento é dada por:

onde :
taer - tempo de aeração (h);
H - altura (m);
va - velocidade do ar (m/h);
vg - velocidade da zona de resfriamento (m/h);
ra - massa volumétrica média do ar (kg/m3);
rg - massa específica do grão (kg/m3);
ca - calor específico médio do ar (kJ/kg,ºC);
cg - calor específico do grão (kJ/kg,ºC).
A massa volumétrica média do ar e o calor específico médio do ar são obtidos através do Diagrama de Mollier.
Os ventiladores utilizados nos processos de aeração são do tipo centrífugo e operam praticamente com velocidade constante. Observando-se as leis que regem seu funcionamento, verifica-se o grande potencial de economia de energia, quando o motor de indução é alimentado por um conversor de freqüência permitindo que o sistema opere com velocidade variável.
As leis de proporcionalidade dos ventiladores centrífugos, ainda que teóricas, podem ser aplicadas com precisão suficiente às condições reais. Para um ventilador com ar à densidade constante, tem-se que a vazão é diretamente proporcional a velocidade no eixo do ventilador, a pressão total, varia com o quadrado da velocidade e a potência desenvolvida é proporcional ao cubo da velocidade (Bose, 1996):

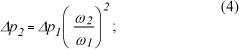

onde :
Q - vazão em m3/h;
Δp - pressão total (mmca);
P - potência desenvolvida (kW);
ω1 - velocidade do eixo do ventilador (rpm);
ω2 - velocidade do eixo do ventilador (rpm).
A potência absorvida da rede é dada por:
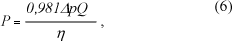
onde (η) é o rendimento total do sistema motor-ventilador.
A energia elétrica consumida em kWh pelo motor durante a operação é :

Desta forma reduzindo-se a velocidade de operação há uma grande redução na potência absorvida e, portanto no consumo de energia (Bose, 1996). É claro que com a redução da vazão é necessário aumentar o tempo de aeração para que a massa de grãos atinja as condições desejadas para o armazenamento porém, através do modelo fuzzy desenvolvido neste trabalho, pode-se determinar um tempo de aeração que não prejudique as características dos grãos e ao mesmo tempo proporcione a maior economia de energia.
Com o sistema operando com velocidade variável, uma redução na velocidade, provoca uma grande redução na potência mecânica e, portanto na potência absorvida da rede de alimentação.
A redução de velocidade é obtida através da diminuição da freqüência da tensão de alimentação do motor. A velocidade de operação de um motor de indução é normalmente próxima a sua velocidade síncrona, a qual é dada por:

Desta forma sendo possível aumentar o tempo de aeração, através da redução da vazão, o que é feito através da redução da velocidade de operação do motor e, portanto, da freqüência do conversor, o consumo de energia cairá drasticamente.
Na Figura 1 são mostradas as curvas que descrevem o comportamento da vazão e da pressão de um ventilador quando o motor opera com velocidade variável, além da curva do comportamento do sistema.
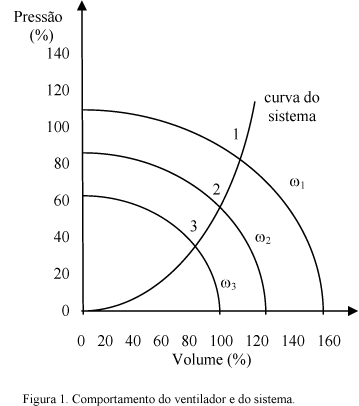
Zadeh (1987), criador da Teoria Fuzzy, demostra em seus trabalhos, a capacidade de tal teoria interpretar os fenômenos não exatos do nosso dia-a-dia, resgatando-os matematicamente de uma forma mais simples e mais exata do que as teorias matemáticas usuais.
Especialistas em programação, como Tanaka & Mizumoto (1974), consideram esta teoria, no que diz respeito aos modelos matemáticos, muito mais adequada a programação, sugerindo softwares de fácil entendimento, capazes de serem usados em várias simulações reais. Isto fez com que a Teoria Fuzzy tenha despertado grande interesse de todos os campos de estudo, e tem sido muito aplicada em controle de processos, modelagem, estimação, identificação e diagnóstico.
MODELO FUZZY PARA OBTENÇÃO DO TEMPO DE AERAÇÃO
Devido à flexibilidade da Teoria Fuzzy, conhecendo-se o comportamento do sistema de aeração que envolve, basicamente, o conjunto motor-ventilador, as propriedades do grão a ser aerado (umidade e temperatura) e as propriedades do ar externo (umidade e temperatura), pode-se compor uma tabela fuzzy de Δθ x U, onde (Δθ) representa a diferença entre a temperatura inicial do grão e a temperatura final de armazenamento desejada, e (U) a umidade do grão. A partir desta tabela e das regras fuzzy determina-se o tempo de aeração necessário para levar a temperatura e a umidade do grão, de seus valores iniciais para os valores desejados de armazenamento.
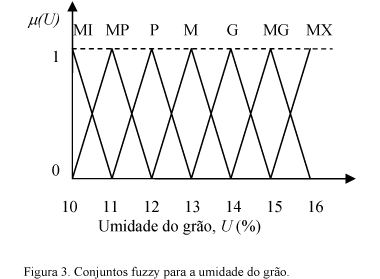
Para a obtenção dos conjuntos fuzzy que representa o comportamento da variação da temperatura (Δθ) e da umidade (U) é necessário, inicialmente, definir os limites inferior e superior de (Δθ) e de (U), bem como a amplitude dos intervalos de variação destas duas grandezas. Estes limites e intervalos são obtidos em função do conhecimento prévio do comportamento das grandezas. Para a variação da temperatura, os limites inferior e superior são de 0º e 24ºC em intervalos de 4ºC. Para a umidade, os limites inferior e superior são de 10 e 16% em intervalos de 1%.
De acordo com a Teoria Fuzzy, cada elemento do conjunto fuzzy possui um grau de pertinência (μ), o qual representa o valor verdade do elemento dentro do conjunto, mostrando o comportamento relativo da grandeza em cada intervalo de variação. O grau de pertinência tem variação entre 0 e 1.
A seguir são apresentados os gráficos da variação da temperatura e da umidade, com seus respectivos conjuntos fuzzy e os graus de pertinência. Os nomes e os símbolos dos conjuntos fuzzy adotados nas Figuras 2 e 3 estão descritos no Quadro 1.
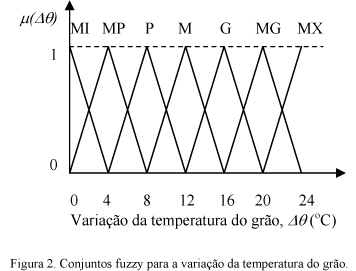

Os índices (I) e (J) identificam os intervalos numéricos de cada conjunto fuzzy das Figuras 2 e 3, respectivamente. Estes índices são calculados através das seguintes equações, onde, "int" significa a parte inteira do valor da expressão :


Pela construção das Figuras 2 e 3, cada elemento (Δθ) ou (U) possui dois graus de pertinência, (μ) e (μ'), onde (μ') é chamado de complementar de (μ). O grau de pertinência (μ) é determinado através do conjunto fuzzy mais à esquerda do elemento e, consequentemente, (μ') relativamente ao conjunto fuzzy mais à direita. Eles são dados por:
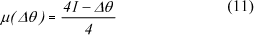

Por definição da Teoria Fuzzy, o grau de pertinência complementar é dado por:
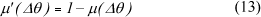
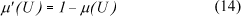
Uma vez calculados os índices (I) e (J) e os graus de pertinência (μ) e (μ'), é necessário aplicar as regras fuzzy. Neste trabalho utiliza-se a regra da interseção, a qual é modelada pela função mínimo, uma vez que o interesse é o "cruzamento" das duas grandezas principais, ou seja, a variação da temperatura e da umidade do grão. Aplicando-se estas regras para a combinação dos graus de pertinência, obtém-se:
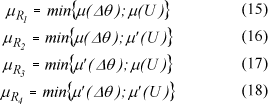
O Quadro 2, que é uma tabela fuzzy U x Δθ e que representa o comportamento do sistema de aeração, é construída analisando o tempo de aeração necessário para atingir uma determinada condição desejada de temperatura e umidade do grão, em função das condições iniciais do grão e do ar externo (temperatura e umidade), das características do sistema de aeração (potência, vazão/pressão) e das características geométricas da célula (seção e altura da massa de grãos). Desta forma, qualquer condição desejada pode ser obtida através do Quadro 2, uma vez que esta tem a flexibilidade para representar qualquer condição, bastando para tanto, alterar as amplitudes dos intervalos das Figuras 2, 3 e 4.
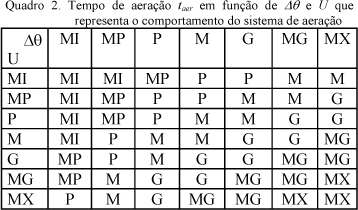
Os nomes e os símbolos dos conjuntos fuzzy adotados para o tempo de aeração (taer) estão descritos no Quadro 3. Os conjuntos fuzzy e a amplitude dos intervalos foram escolhidos conforme o comportamento do sistema de aeração e estão representados na Figura 4.

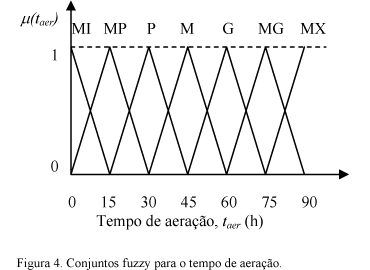
A recuperação da importância do tempo de aeração (ti), correspondente a cada regra fuzzy (μRi ), é feita utilizando-se o Quadro 2 e calculados pelas equações (19) a (22). Para cada par ordenado (U,Δθ), obtém-se o correspondente conjunto fuzzy para (ti), ao qual será atribuído um valor, conforme o Quadro 3. Os símbolos acompanhados do sinal (´), representam o conjunto fuzzy complementar.
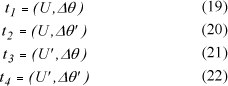
O cálculo do valor do tempo de aeração (taer) é dado pelo método de defuzzyficação (centro de massa).
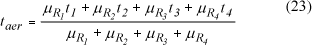
MODELO FUZZY PARA OBTENÇÃO DA FREQÜÊNCIA
Para a determinação da freqüência de operação do conversor, serão utilizados os conjuntos fuzzy da variação da temperatura (Δθ) e do acréscimo do tempo de aeração (Δtaer). O conjunto (Δθ) é o mesmo já definido anteriormente. Para o conjunto (Δtaer) são definidos os limites inferior e superior de 0 e 60 horas, bem como os intervalos de variação de 10 horas, os quais estão representados na Figura 5.

Os nomes e os símbolos dos conjuntos fuzzy adotados na Figura 5 estão descritos no Quadro 4.

O índice K que identifica os intervalos numéricos de cada conjunto fuzzy para (Δtaer) é calculado por:
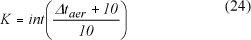
O grau de pertinência μ(Δtaer) para cada elemento (Δtaer) da Figura 5, pertencente ao conjunto fuzzy mais à esquerda, é calculado por:
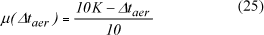
O grau de pertinência para o elemento complementar é dado por:
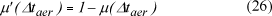
Com o cálculo do índice (K) e os graus de pertinência μ(Δtaer) e μ'(Δtaer), aplica-se às regras fuzzy para a combinação dos graus de pertinência, obtendo-se:
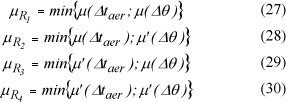
O Quadro 5, que é uma tabela fuzzy Δθ x Δtaer, e que representa o comportamento da freqüência do conversor que aciona o motor do sistema de aeração do silo, é construída analisando-se, a velocidade do motor, a nova vazão específica e as alterações de temperatura e umidade na massa de grão ensilada.

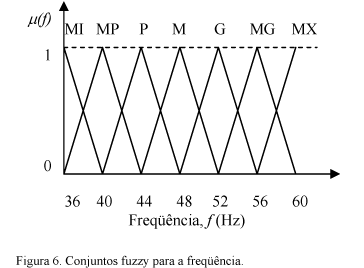
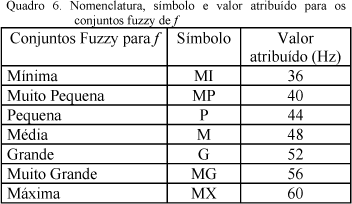
Os conjuntos fuzzy e a amplitude dos intervalos foram escolhidos conforme o comportamento do sistema e estão representados na Figura 6. Os nomes e os símbolos dos conjuntos fuzzy adotados para a freqüência do conversor (f) estão descritos na Quadro 6.
O valor da freqüência (fi), correspondente a cada regra fuzzy (μRi ), é feita utilizando-se o Quadro 5 e as equações (31) a (34). Para cada par ordenado (Δθ,Δtaer) obtém-se o correspondente conjunto fuzzy para cada (fi), ao qual é atribuído um valor conforme o Quadro 6. Os símbolos acompanhados do sinal (´), representam o conjunto fuzzy complementar.
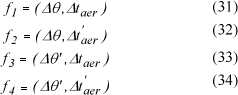
O cálculo do valor da freqüência do conversor (f), é dado por:
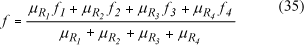
RESULTADOS E DISCUSSÃO
Na Figura 7, apresenta-se o cálculo da freqüência em função do acréscimo no tempo de aeração.
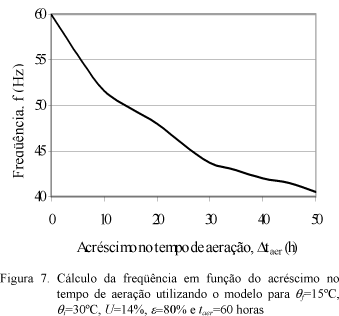
Na simulação apresentada, supõe-se que a massa de grãos deverá ser armazenada com uma temperatura final θf=15ºC e umidade de U=14%. Admitem-se que a temperatura inicial do grão atinja θi=30ºC, ou seja, por algum motivo a massa de grãos sofreu um aquecimento e, portanto, deve ser aerada para retornar as condições iniciais.
O tempo de aeração necessário para tal condição é, então, calculado pelo modelo, obtendo-se o valor taer=60 horas, para a temperatura média do ar externo θar=25ºC e sua umidade relativa média de ε=80% quando o motor de indução opera com freqüência nominal de 60Hz. Para esta situação, o consumo de energia elétrica é de 751,4kWh e a vazão total é de 5100m3/h.
Conhecido o tempo de aeração de referência, o operador poderá optar em aumentar o tempo de aeração, por exemplo, em mais 15 horas, com o objetivo de reduzir o consumo de energia elétrica. Uma vez definido qual será o acréscimo no tempo de aeração, automaticamente, o modelo calculará a freqüência necessária para que isso aconteça, que, no caso, seria f=50Hz.
A finalidade de reduzir a freqüência é a redução do consumo de energia elétrica. A redução da freqüência através do conversor proporciona uma redução da velocidade do motor, o que provoca uma grande redução da potência elétrica absorvida da rede de alimentação, fazendo com que ocorra uma expressiva redução no consumo de energia elétrica.
É importante ressaltar que, aumentar o tempo de aeração com a finalidade de reduzir o consumo de energia elétrica, depende das necessidades e prioridades de cada operador.
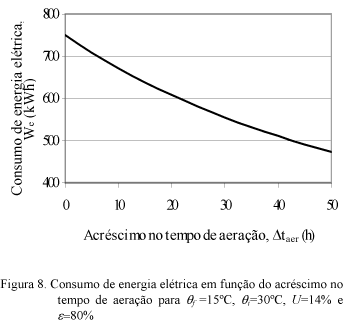
Na Figura 8, apresenta-se o consumo de energia elétrica em função do acréscimo no tempo de aeração. Quanto maior o acréscimo no tempo de aeração, menor poderá ser a freqüência da tensão do motor de indução e, consequentemente, menor o consumo de energia elétrica.
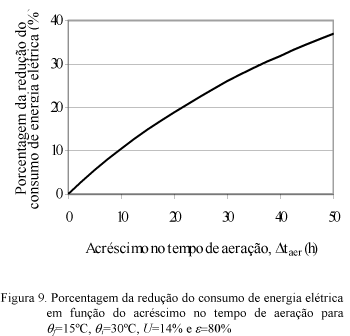
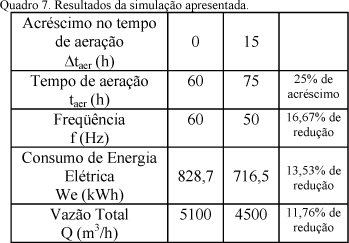
Comparativamente, a Figura 9 mostra a porcentagem de economia do consumo de energia elétrica em função do acréscimo no tempo de aeração. Observa-se que, quanto maior o acréscimo no tempo de aeração, significativos índices de economia do consumo de energia elétrica são obtidos. Para a simulação descrita anteriormente, um acréscimo de 15 horas acarretará em uma economia de 13,53% no consumo de energia elétrica. O Quadro 7 resume a simulação apresentada.
CONCLUSÃO
O tempo de aeração calculado pelo modelo desenvolvido, bem como pelos métodos convencionais, é um tempo provável para que a massa de grãos ensilada atinja as condições desejadas de armazenamento. Praticamente, é impossível determinar um tempo exato de aeração, pois muitos são os fatores que influenciam neste cálculo e, sendo estes fenômenos físicos, como os climáticos, são impossíveis de serem controlados. Levando-se em consideração os fatos acima, o modelo desenvolvido mostra-se confiável e eficiente no cálculo do tempo de aeração, apresentando resultados compatíveis com os da literatura citada. O modelo é simples, de fácil compreensão e implementação, se comparado aos convencionais. Sua capacidade de interpretar fenômenos físicos com maior precisão também é uma de suas vantagens, cujo mérito se deve totalmente à Teoria Fuzzy.
Os resultados apresentados mostram que o modelo é capaz de oferecer a possibilidade da redução do consumo de energia elétrica. Ao se optar por um acréscimo no tempo de aeração, o modelo fornece a freqüência necessária que deve ser aplicada ao motor de indução, com a confiabilidade de que a nova vazão obtida, apesar de menor, é suficiente para que a zona de resfriamento atinja as últimas camadas em tempo hábil. É evidente que o tempo de aeração não pode ser aumentado indefinidamente, mas até quanto for possível, o modelo é capaz de fornecer a freqüência necessária para tanto. O modelo prevê um acréscimo máximo no tempo de aeração de até 60 horas. Este limite máximo parece ser razoável em face ao tempo de aeração e aos valores da redução da freqüência e da vazão total obtidos nas simulações. Ressalta-se, entretanto, que qualquer acréscimo no tempo de aeração acarretará redução do consumo de energia elétrica.
De uma forma geral, o modelo desenvolvido comporta-se muito bem quando comparado aos modelos convencionais. Demostra ser eficiente em atender os objetivos previstos neste trabalho, além de trazer uma contribuição significativa para os sistemas de aeração em silos verticais. A nova tecnologia apresentada, toda ela baseada na Teoria Fuzzy, deve ser explorada, com o intuito de oferecer novos conceitos, abrir diferentes caminhos e vislumbrar novas possibilidades. O modelo desenvolvido deixa a possibilidade da construção do controlador fuzzy, o qual é responsável pela atuação do modelo no sistema de aeração em silos verticais.
REFERÊNCIAS BIBLIOGRÁFICAS
[1] BOSE, B. K. Expert system, fuzzy logic, and neural networks in power electronics and drives, Power Electronics and Variable Frequency Drives, IEEE Press, NJ: 1996, p. 559-627.
[2] BURREL, N. J. Aeration Systems, London Road: Ministry of Agriculture, Fisheries and Food, 1973, 45p.
[3] LASSERAN, J. C. Aeração de grãos, CENTREINAR, nº. 2, Viçosa, 1981, 131p.
[4] TANAKA, K. AND MIZUMOTO, M. Fuzzy programs and their execution, Fuzzy Sets and their Applications to Cognitive and Decision Processes, Academic Press, NY: 1974, p. 41-76.
[5] ZADEH, L. A. Fuzzy Sets and Applications, John Wiley & Sons, USA: 1987, 648p.










 How to cite this paper
How to cite this paper