An. 4. Enc. Energ. Meio Rural 2002
Análise de risco envolvido no projeto de cogeração de energia à gás natural utilizando o método Monte Carlo de simulação estocástica
Campelo, R.C*; Santos, H. P. A; Costa, G. B; Pannir, S. P.V.
Universidade Federal do Rio Grande do Norte. Departamento de Engenharia Química - GPEC. Fone: (084) 215-3769 FAX: (084) 215-3770. www.gpecufrn.hpg.com.br e-mail: ronaldo@eq.ufrn.br
RESUMO
Tendo em vista, hoje em dia, a importância da cogeração e os seus benefícios já comprovados em grande escala, esse trabalho trata da aplicação do método Monte Carlo à análise de risco de sistemas de cogeração em pequena escala. Os sistemas de cogeração prevêem a utilização simultânea da energia mecânica e da energia térmica provenientes de uma única fonte de energia primária. Utilizando um motor de combustão interna movido a gás natural, a energia térmica produzida será aproveitada para gerar vapor, podendo este ser utilizado em diversas aplicações. Inicialmente, foi realizada a síntese do projeto, os balanços de massa e energia para o processo e, com auxílio de programas de computador que fazem regressões e simulações, os equipamentos foram dimensionados e especificados, sendo determinada, também, a função lucro para o processo. Posteriormente, foi realizada a análise risco econômico, variando-se as condições de operação do motor-gerador que por conseqüência altera o consumo de matéria prima e de produtos. A simulação estocástica foi desenvolvida utilizando-se planilha eletrônica baseada em métodos de distribuição de incerteza e o software @Risk, simulador Monte Carlo. Os resultados deste trabalho mostram que a probabilidade de se obter lucro nesse processo é me torno de 30%.
Palavras Chaves: Cogeração; Simulação; Monte Carlo; Geração de vapor.
ABSTRACT
In view of the present day proven importance of the cogeneration and its benefits in large-scale, this work deals with the application of the Monte Carlo method to the analysis of risk of systems of cogeneration in small scale. The cogeneration systems foresee the simultaneous use of the mechanical and thermal energy proceeding from an only primary energy fonts. Using an engine of internal combustion running with the natural gas, the produced thermal energy will be used to advantage to generate steam, this can used in diverse aplications. Initially, the synthesis of the project was realized, the mass and energy balance was carried out and, with aid of computer programs that they make regressions and simulations, the equipments size were specified, being certain, also, the function profit for the process. Later, the analysis economical risk was accomplished, being varied the conditions of operation of the motor-generator that for consequence alters the matter consumption it excels and of products. The stochastic simulation was developed being used electronic spreadsheet based on methods of uncertainty distribution and the software @Risk, simulator Monte Carlo. The results of this work show that the probability of obtaining profit in that process is me I turn of 30%.
INTRODUÇÃO
Tendo em vista a importância que as fontes energéticas naturais e não renováveis têm para o homem, se torna cada vez maior a preocupação com a conservação delas. Aliado a este fato, a globalização da economia exige das empresas maior competitividade, visando a melhoria do rendimento energético do ciclo produtivo. Nesse contexto estão inseridos os sistemas de cogeração, hoje amplamente utilizados em países desenvolvidos, ao contrário do Brasil que se encontra em estágio inicial de desenvolvimento. Nesse trabalho o objetivo é desenvolver um projeto de cogeração de energia em pequena escala, utilizando um motor de combustão interna que tem como combustível o gás natural. A energia térmica produzida terá, a princípio, a finalidade de gerar vapor, podendo este ser utilizado para secagem de frutas, por exemplo. O projeto preliminar desenvolvido teve o auxílio de softwares que ajudam na modelagem do processo com balanço de massa e no dimensionamento dos equipamentos utilizados.
Na simulação são utilizados softwares com modelos computacionais para processos, no qual se introduz a condição desejada de operação (mais provável de ocorrer) e de alimentação (vazões e concentrações). Nesse caso, tendo em vista que o projeto é de pequena escala, essas condições foram ajustadas de forma que a quantidade de energia elétrica gerada não fosse muito grande.
REVISÃO BIBLIOGRÁFICA
TIPOS DE SISTEMAS DE COGERAÇÃO
Os sistemas são basicamente separados em dois grandes grupos, em função da seqüência de utilização da energia, podendo ser de "topping cycle" e "bottoming cycle". Nos sistemas tipo "topping cycle" o energético, (gás natural, por exemplo) é usado primeiramente na produção de energia elétrica (ou mecânica) em turbinas ou motores a gás e o calor rejeitado é recuperado para o sistema térmico. Nos sistemas com "bottoming cycle" o energético produz primeiramente vapor, que depois de utilizado para produção de energia mecânica (e/ou elétrica) em turbinas a vapor, é repassado ao processo.
A escolha de uma das soluções acima é função do perfil de necessidades elétricas e térmicas de cada aplicação. Os sistemas "topping cycle" são de emprego mais amplo e mais difundidos, podendo empregar turbinas ou motores a gás (ou a diesel).
MOTORES A GÁS
Em geral, os motores a gás apresentam uma eficiência elétrica maior do que as turbinas a gás, conseguindo converter algo ao redor de 32% a 40% da energia do combustível em energia mecânica, enquanto as turbinas conseguem tipicamente de 22% a 35% (turbinas de maior porte conseguem atingir eficiências maiores, chegando em alguns casos a 40%).
APLICAÇÕES DA COGERAÇÃO
O campo de aplicação dos sistemas de cogeração é bastante vasto, tanto no setor industrial quanto no terciário. Os usuários com o maior potencial de aplicação e rentabilidade são aqueles que operam seus sistemas em regime de 24 horas, com elevado consumo de eletricidade e calor. Na área industrial são possíveis, por exemplo, os seguintes usos:
-Geração de vapor de baixa, media e alta pressão.
-Calor direto da turbina para ar de alimentação de fornos
-Secagem de grãos e de produtos
-Aquecimento de óleos e fluidos industriais
No setor terciário pode-se aplicar a cogeração em hotéis, hospitais, centros de processamento de dados, shopping centers, edifícios comerciais, etc. Nestes casos o calor de descarga poderá ser empregado para geração de vapor e/ou água quente para aquecimento (ambiental ou de água predial), para cozinhas, etc.
2.4 Ciclo de Carnot
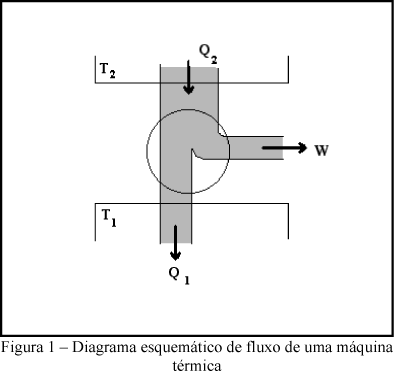
Em 1824, Carnot introduziu na teoria da termodinâmica um processo cíclico simples, agora conhecido como o ciclo de Carnot. Pode-se dizer que seu trabalho estabeleceu os fundamentos das ciências termodinâmicas. Sua principal utilidade é auxiliar o raciocínio termodinâmico. As características marcantes do Ciclo de Carnot são: (a) todo fluxo de calor (Q2) para o sistema tem lugar a uma só temperatura mais alta T2; (b) todo fluxo de calor (Q1) saindo do sistema tem lugar a uma só temperatura inferior T1; (c) o sistema, freqüentemente chamado de substância operante, executa um processo cíclico; e (d) todos os processos são reversíveis. Em geral, qualquer processo cíclico limitado por dois processos isotérmicos reversíveis e dois processos adiabáticos reversíveis constitui um Ciclo de Carnot.
Embora as magnitudes dos fluxos de calor e do trabalho sejam arbitrárias, encontra-se a razão Q2/Q1 só depende das temperaturas T2 e T1. Para calcular esta razão é necessário conhecer a equação do estado do sistema e sua equação da energia. Para o gás ideal, por exemplo, temos a equação (1).

A MÁQUINA TÉRMICA
Um sistema submetido a um Ciclo de Carnot é o protótipo de todas as máquinas térmicas cíclicas. A característica comum a todos estes dispositivos é que eles recebem uma alimentação de calor a uma ou mais temperaturas mais altas, realizam trabalho mecânico sobre suas vizinhanças e liberam calor a alguma temperatura mais baixa.
O rendimento térmico η de uma máquina térmica é definido como a razão do trabalho produzido W pelo calor fornecido ao sistema Q2 como se vê em (2):
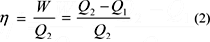
Essa definição se aplica a qualquer tipo de máquina térmica e não se restringe a uma máquina de Carnot. É proveitos representar a operação de qualquer máquina térmica por um diagrama de fluxo, conforme mostra a figura 1.
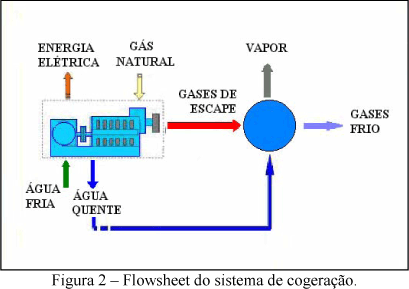
METODOLOGIA
SIMULAÇÃO DO PROCESSO E SISTEMA PROPOSTO PARA O ESTUDO DE CASO
Para a realização deste trabalho foram utilizados os softwares SuperPro Designer, @Risk for Excel e Statistc com a finalidade de realizar a simulação do sistema de cogeração com geração de vapor em pequena escala. Antes de se iniciar a simulação propriamente dita, realizou-se a síntese do processo e para isso foi necessário pesquisar a respeito dos equipamentos mais adequados e suas variáveis de operação. O sistema consiste basicamente de dois equipamentos principais: o motor-gerador e o trocador de calor. A idéia é aproveitar ao máximo a energia produzida pela combustão do gás natural, aumentando o rendimento energético. Para isso, a água que será utilizada para gerar vapor é a que sai da jaqueta de resfriamento do motor e por isso, já está pré-aquecida (82°C). A alta temperatura dos gases de escape também se deve a combustão do gás natural que transfere grande quantidade de energia para os gases de exausto. A seguir é mostrado um flowsheet do sistema proposto (Figura 2).
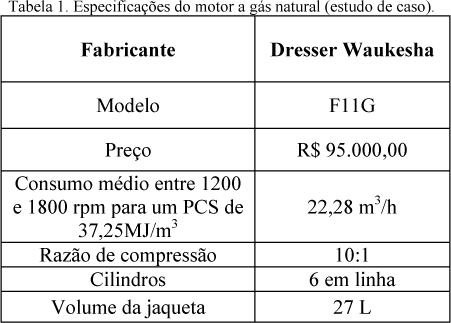
O motor-gerador proposto para atender às necessidades elétricas e térmicas, neste caso, é especificado na tabela 1, a seguir.
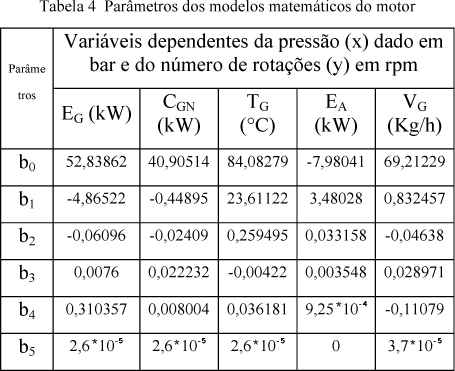
Dados empíricos obtidos a partir do motor especificado, forneceram modelos matemáticos a partir de regressões realizadas no software Statistica pelo método quasi-Newton.
As variáveis de saída dependem basicamente de duas variáveis de operação do motor, são elas: o número de rotações e a pressão. Dessa forma, os modelos obtidos são como mostrado na equação (1).
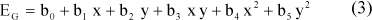
Onde x é a pressão (bar) e y o número de rotações (rpm). EG é a energia no exausto, e uma das variáveis dependentes. As demais variáveis dependentes são obtidas utilizando o mesmo modelo,são elas: o consumo de gás natural (CGN), a temperatura dos gases de exausto (TG), a energia transmitida para a água de resfriamento (EA) e a vazão de gases no exausto (VG).
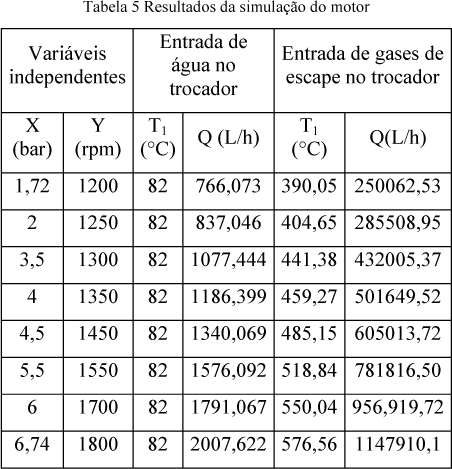
Com esses modelos foi possível fazer simulações (num total de oito) com valores aleatórios de pressão e rotação dentro dos limites do motor, incluindo o máximo e o mínimo. Com esses modelos foi possível determinar o rendimento global do sistema (tabela 2), ou seja, o aproveitamento da energia gerada pela combustão do gás natural.
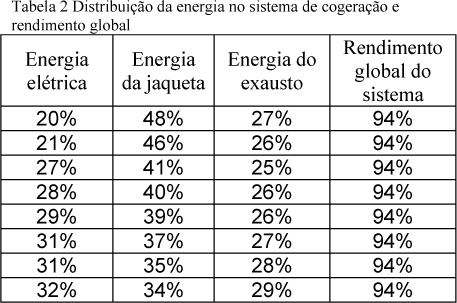
De posse dos resultados dessas simulações, também foi possível simular, utilizando o software SuperPro Designer 4.5, a troca de calor entre os gases do exausto e a água de resfriamento do motor, que segundo o fabricante, em condições padrões, sempre deixa a jaqueta com 82°C. Dessas simulações foi possível obter a quantidade de vapor gerado, considerada, juntamente com a energia elétrica, neste caso, como produto.
Para a simulação do processo utilizou-se a seguinte seqüência:
- Iniciou-se, utilizando bancos de dados do Simulador Super Pro, as substâncias e os agentes de transferência de calor que são utilizados durante o processo;
- Selecionaram-se os equipamentos utilizados no processo;
- Discriminaram-se as informações sobre as correntes de entrada e os parâmetros de processo;
- Efetuou-se a simulação do processo, realizando automaticamente as cálculos de balanço de massa, balanço energético e informações das correntes de saída.
SIMULAÇÃO ESTOCÁSTICA DO PROCESSO UTILIZANDO O MÉTODO MONTE CARLO
Considerando que no processo seja consumido apenas gás natural e produzido vapor e energia elétrica, foram estabelecidas V1, V2 e V3 como sendo as variáveis estocásticas, onde seus valores podem ser obtidos pelas equações (3), (4) e (5) respectivamente.
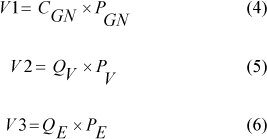
Onde CGN é o consumo de gás natural em m3/h, QV a quantidade de vapor produzida em ton/h, QE a quantidade energia produzida em PGN o seu respectivo preço em R$/m3.
Sabendo que o lucro depende diretamente das variáveis de produção conforme a equação (6), foi construída uma tabela onde os maiores valores (+) e menores valores (-) de cada variável são distribuídos de forma a realizar todas as combinações possíveis entre eles (tabela 3), obtendo para cada linha da tabela um valor diferente para o lucro.
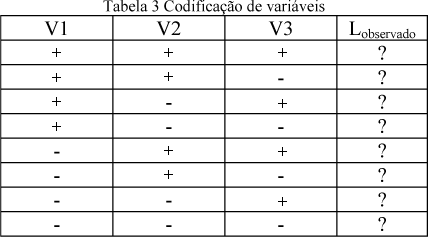
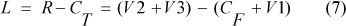
Onde CF é o custo fixo unitário (custo de capital, manutenções, e outros que não dependem da produção) e CT é o custo total. Comparando o segundo termo da equação (6) com o terceiro, pode-se perceber que a soma de V2 e V3 é a receita e V1 é igual ao custo variável. Dessa forma fica claro como as varáveis V1, V2 e V3 interferem no valor do lucro.
Com o objetivo de determinar como o lucro se comporta em função das três variáveis de produção, foi realizada uma nova regressão utilizando o Statistica, e também pelo método quasi-Newton, obteve-se uma modelo, chamado de função lucro ou objetiva.
Obtida a função, ela foi levada ao simulador @Risk 4.5 for excel que realizou simulações estocásticas, ou seja, atribuiu valores aleatórios para as variáveis V1,V2 e V3 e através da função objetiva determinou o valor do lucro. Dada a rapidez e praticidade com que o software executa tal tarefa e a fim de se obter uma boa amostragem, pediu-se que ele executasse mil simulações.
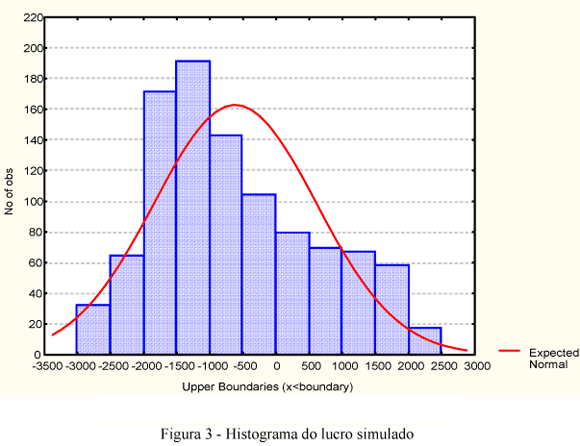
Em seguida, foi plotado um histograma com quinhentos pontos dentre os mil simulados, para que se observasse a porcentagem em que se obtém um lucro satisfatório.
RESULTADOS E DISCUSSÕES
OBTENÇÃO DOS MODELOS PARA O MOTOR À GÁS
A seguir, na tabela, são mostrados os valores dos parâmetros de b0 a b5 para cada variável de saída do motor.
SIMULAÇÃO DO MOTOR E DO TROCADOR DE CALOR
Para realizar a simulação do motor foram lançados, de forma aleatória, valores de pressão (x), e número de rotações (y). Estes valores abrangem os limites máximos e mínimos de cada uma das duas variáveis especificados pelo fabricante, sem, contudo, ultrapassa-los. Os resultados das simulações (realizadas utilizando os modelos matemáticos obtidos para o motor) forneceram os dados para a simulação do trocador de calor utilizando o SuperPro Designer (tabela 5 e 6).
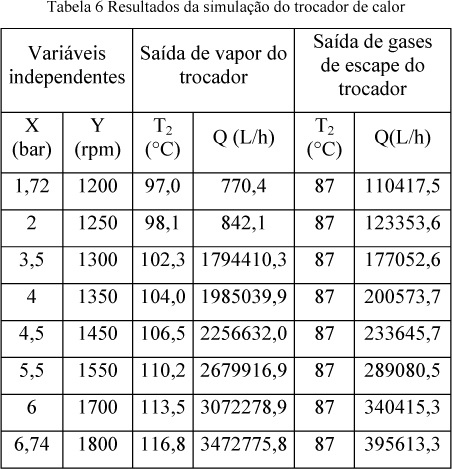
Pode-se observar na tabela 6 que para as duas primeiras simulações, a temperatura dos gases de escape não é suficiente para a geração de vapor, obtendo-se líquido saturado.
SIMULAÇÃO DETERMINÍSTICA
A partir das equações (3), (4) e (5), pôde-se obter os valores mínimos e máximos de V1, V2 e V3 que são respectivamente 2,0455 e 7,5449, 823,8622 e 1585,7207 e 0,1404 e 0,8276. O valor do lucro foi determinado de acordo com a combinação dos valores das variáveis estocásticas. O custo fixo unitário foi estimado em R$ 5,3161. Os resultados das simulações determinísticas são mostradas na tabela 7.
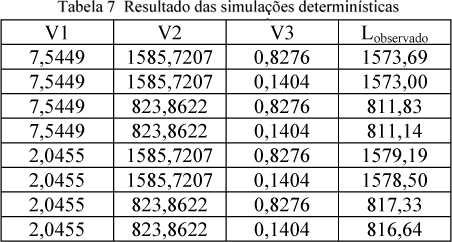
Realizada a regressão com os valores da tabela 7, foi obtido a equação (8) que é a função lucro para o processo.
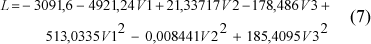
A partir dos valores gerados de forma randômica pelo simulador foram calculados mil valores para o lucro, dos quais quinhentos deram origem ao histograma ilustrado na figura 3.
CONCLUSÕES
Com base nas simulações realizadas concluiu-se que para o projeto tornar-se viável economicamente é necessário que o motor-gerador esteja operando em condições de proporcionar, aos gases de escape, temperaturas acima dos 440°C.
A probabilidade de se obter lucro, para as simulações realizadas, é de cerca de 30% o que pode ser considerada significativa.
Os resultados deste caso mostram que o método de simulação estocástica é uma excelente ferramenta para avaliação de comportamento de geração de energia elétrica num ambiente de incerteza com diversas variáveis, principalmente preços de combustível.
O modelo apresentado por ser aproveitado para outros processos de cogeração, com escalas diferentes.
AGRADECIMENTOS
Agradecemos à Agência Nacional de Petróleo (ANP/PRH-14) pelo apoio através da bolsa de pesquisa em nível de iniciação científica, ao CNPq e a todos que contribuíram para o desenvolvimento deste trabalho.
BIBLIOGRAFIA
CHOPEY, N. P. Handbook of Chemical Engineering Calculations - McGraw Hill, 2 ed., 1993.
COLLINS, S. Combustion Technology, In: Encyclopedia of Chemical Technology, vol. 6 ed. Willy Interscience, New York, 1989.
FONTES Jr, A. O., Avaliação do Comportamento de um Motor Diesel de Dois Cilindros Convertido para Ciclo Otto, Utilizando Gás Natural Veicular, dissertação de mestrado - Dept.
HORLOCK J. H.. Cogeneration Combined Heat and Power 2 ed. Malabar, Flórida: Krieger Publishing Company, 1997.
JALURIA Y. Design and Optimization of Thermal Systems - McGraw Hill International Editions, Mechanical Engineering Series, 1998.
MATLEY, J., (1984), Modern Cost Engineering: Methods and Data, Chemical Engineering, Mc Graw Hill Publications, V. 2, p. 265-269, New York.
ROSA(1) R. A. SILVA(2) A. A. Motores a gás e recuperação de CO2 a melhor eficiência em cogeração - Recife, 10 de Julho de 2000 - disponível em <http://www.gasnet.com.br.> (1) Project Manager - The Wittemann Company; (2) Eng.ª Mecânica Chefe do Setor Comercial da ALGÁS S/A - AL.
SELVAM, P.V.P. CORTEZ, I.R. et alli Estudo de Engenharia de Processo e Custo para Valorização de Biogás via Cogeração de Energia Auxiliado por Computador - Congresso Brasileiro de Engenharia Química, 2000.
SELVAM, P. V. P et al. Simulação Estocástica do Processo de Produção de Etanol usando cana de açúcar. Anais V. Seminário de Hidrólise Enzimática de Biomassa. Maringá - PR, 1996.
SELVAM, P.V.P., Desenvolvimento e implantação do método Monte Carlo de simulação para processo de produção de reatores, Anais do 10° Congresso Brasileiro de Engenharia Química, 1, p. 846-851, São Paulo (1994)
YOKOYAMA, R. ITO, K. Optimal Operational Planning of Cogeneration Systems with Thermal Storage by the Decomposition Method - Journal of Energy Resources Technology, vol. 117 / 337, p.337-342. Japão, Dezembro 1995.










 How to cite this paper
How to cite this paper