An. 4. Enc. Energ. Meio Rural 2002
Fuel ethanol from Brazilian biomass: economic risk analysis based on monte carlo simulation techniques
Nøvaes1, W. S.; Caixeta, S. H. M; Selvam, P. V. P.; Santos, H. P. A.; Costa, G. B.
Universidade Federal do Rio Grande Norte - UFRN, Núcleo de Tecnologia - NT. Programa de Pós - Graduação em Engenharia Química - PPGEQ, Grupo de Pesquisa em Engenharia de Custos e Processos - GPEC, Campus Universitário - Lagoa Nova, CEP: 59072 - 970 - Natal/RN. Home Page: www.ufrngpec.hpg.com.br; E - Mail: alquimista@eq.ufrn.br1
ABSTRACT
At the present the fuel ethanol from Brazilian biomass is one of the most favorable energetic project in development to the Brazil mainly with respect to the rural employment, environment and energetic safety. In this context, a technological and economical study was developed applied to fuel ethanol production from sugar cane based on dynamic modeling, simulations and economical risk analysis. The objective of this work concern to develop an stochastic methodology and as well as the implementation of the economic risk analysis inherent to the ethanol process production by the changing of the process variables and parameters based on Monte Carlo simulation method. The mass balance and economic evaluation was obtained from simulations were carried out using the SuperPro DesigneTM v. 3.0 software. In addition to this, the economic risk analysis was carried out based on changing in the distribution of the selling price, yield of fermentation and feed flow rate the process stochastic variables. The stochastic analysis using Monte Carlo simulation was implemented in a spreadsheet model utilizing @Risk v. 4.5 software for Excel. Based on deterministic and stochastic simulations of the fuel ethanol production the results saveral techn economical parameters have been obtained and analyzed. The important advantage of the proposed method is the possibility to predict the economical risk involved in the ethanol production take in to account the aleatory and complex nature inherent to the process, with precision, reliability and very rapidly.
Key words: Ethanol, Simulation, Stochastic, Monte Carlo, Risk Analysis.
RESUMO
O etanol derivado da biomassa brasileira constitui hoje um dos projetos energéticos mais propícios em desenvolvimento para o Brasil, principalmente no que diz respeito ao emprego rural, ao meio ambiente e a segurança energética. Pensando nisso, desenvolvemos um estudo tecnológico e econômico sobre a produção de etanol derivado da cana - de - açúcar, utilizando modelagem dinâmica, simulação e análise de risco econômico através de métodos estocásticos. O objetivo do presente trabalho consiste em desenvolver um modelo estocástico para a simulação e também a implementação da análise de risco econômico envolvido no projeto, devido à variação de parâmetros e variáveis de processo através do método Monte Carlo de simulação estocástica. O balanço de massa e a avaliação econômica foram obtidos através de simulações, utilizando para isso o software SuperProTM Designer v.3.0. Realizou-se, também, a análise de risco econômico variando o preço de venda, rendimento de fermentação e a capacidade de produção, consideradas como variáveis estocásticas do processo. Desenvolvemos a simulação estocástica utilizando planilha eletrônica baseada em métodos de distribuição de incerteza e o software @Risk, simulador Monte Carlo. Através da simulação do processo de produção de etanol combustível, foram obtidos como resultados os investimentos necessários, os lucros e o retorno sobre os investimentos. Pelos resultados obtidos, podemos concluir que por meio de nossas simulações e análise de tais resultados, que através do método Monte Carlo é possível realizar uma modelagem considerando a natureza aleatória e complexa inerente a cada processo químico, com rapidez, precisão e confiabilidade dos resultados obtidos.
Palavras chaves: Etanol combustível, Simulação, Estocástica, Monte Carlo, Análise de Risco.
INTRODUCTION
The increasing capability of computer processing has facilitated the development and use of software to simulate chemical and others industrial process. The procedure of process simulation consist in the resolution of the set of mathematical relations that describe system behaviour, for example, mass and energy balance, phase equilibrium equations, physical properties calculations, etc. Where as such mathematical model contains input variables, process parameters and output variables. The traditional simulation approach involve definition on input variables and process parameters, thus output variables are evaluated by use of the model, which produces deterministic (point estimate) results for um particular set of assumptions. (MIZUTANI et al, 2000)
Fuel ethanol production industries are usually faced with uncertain conditions during their operation. These uncertain can arise from variations either in external parameters, such as the quantity of feed streams, temperature and concentration, or internal process parameters such transfer coefficients, reactions constants, physical properties and as well as price of fuel ethanol because of variation in fuel price market. If the technology is new, there are additional uncertainties due to limited performance data. Thus, utilisation of the deterministic simulation results can be limited due to the uncertainties associated with the variables and parameters in the real process and the solution of the model can be significant from the real process response. Therefore, an efficient and systematic method is required to evaluate uncertainties and investigate the effect of the uncertainties in chemical process simulation.
An approach tool widely used for uncertainty analysis employs the concept of stochastic analysis simulation (DIWEKAR and RUBIN, 1991). This approach is based on a large number of simulation runs, in each run, input variables and process parameters are randomly selected according to adequate probability density functions. The set of out put variables evaluated gives important information about the behaviour of the statistical process, indicating the most probable variable range.
In short, the process analysis of real systems requires both stochastic and deterministic modelling capabilities. Yet, not much works have been realised in Brazil about stochastic modelling applied to fuel ethanol production even though Brazil is the leader in this field.
Thus, the objective of this paper is to develop a generalised stochastic modelling methodology applied to uncertainties analysis inherent to the fuel ethanol process production aided for deterministic simulator and stochastic spreadsheet models based on Monte Carlo simulation techniques.
DETERMINISTIC ANALYSIS
The modelling tools in current simulators may roughly classified into two groups, block-oriented (or modular) and equations-oriented approaches. (MARQUARDT, 1996)
Block-oriented approach mainly addresses modelling on the flowsheet level. Every process is abstracted by a block diagram consisting of standardised blocks, which model behaviour of a process unit or part of it. All the blocks are linked by single-like connections representing the flow of information, materials and energy employing standardised interface and stream formats.
Models of process unit are preceded by one model expert and incorporated in a model library for later use. Modelling on the flowsheet level is either supported by one modelling language or by a graphical editor. In both cases, the end user select the models from the library, provides the model parameters and connects them to the plant model. The incorporated chemical engineering knowledge as well as the model structure are largely fixed and not accessible. Common exceptions are physical property models, which can be selected independently of the process unit model.
Equation-oriented modelling tool support the implementation of unit models and their incorporation in a model library by means of declarative modelling language or by providing a set of subroutine templates to be complete directory in a procedural programming language. There are no different tools for modelling expert or for the end user. Hence, modelling on the unit level requires profound knowledge in such diverse areas as chemical engineering, modelling and simulation, numerical mathematics, and computer science. The development of novel process unit models is therefore often restrict to a small group of expert.
Theses later approaches do not many advantage compared to the modular modelling tool meanly in the implementation complexity because the equation-modular approaches requires a high computational and technical knowledge.
The SuperPro DesignerTM v.3.0 software has been the computational tool used in this study. The SuperPro Designer is part of the block-oriented simulator group. It is comprehensive computer simulations package the fate of chemicals in individual and combinations of unit operation. A list of these chemicals that is global to the process flowsheet is specified from an extensive database provided with the software. User-defined chemicals can be added of this database. The process diagram is built in a "point and click" CAD environment by adding unit operation to a flowsheet and establishing the connectivity between these units using streams. The chemical components of the streams that serve as influent to the whole process are defined. (INTELLIGEN, 1994 and 1998)
The consecutive unit operations are solved using sequential mass balances where the effluent streams from one unit operation serves as the influent streams to another unit operation. (INTELLIGEN, 1994 and 1998)
Results of the simulation can be viewed by clicking directly on stream or unit operation on the screen. Comprehensive output can be obtained by generating stream and input data report that can be viewed in separating windows. (INTELLIGEN, 1994 and 1998)
Beyond mass balance, SuperPro Designer has the capacity to perform economical analysis to evaluate the capital and operating costs of different flow diagrams, and the capacity to schedule batch operations. The steps to take place one deterministic simulation approach using the SuperPro Designer are the following. (INTELLIGEN, 1998)
- Draw out the flowsheet;
- Define the components;
- Select the thermodynamic calculation method;
- Define the feed streams;
- Provide process conditions for the unit operation;
- Run the simulation.
STOCHASTIC ANALYSIS
In general, uncertainty analysis requires stochastic modelling environments. Some papers (LEE et al, 1996) classify the Monte Carlo (MC) analysis like one of the most widely used approach, which implies two steps of applications. One is distribution sampling from one distribution to estimate other distribution. The other is using the distribution sampling technique to solve a probabilistic problem, which is generated from a deterministic problem. This approach has been successfully applied to calculation of complex integrals, solutions of equations, etc. the advantage of this approach is flexibility. First, its implementation is very easy, and modification of model is not necessary. Second, various independent and dependent variables are considered simultaneously. Third, various numerical and graphical technique can be used for analysis of relationship between the model inputs and outputs.
Generally, simulation based on Monte Carlo simulation analysis is performed through the following six steps.
- Functional or mathematical model is defined;
- Probability distribution function are allocated to design and/or input variables;
- Random samples are generated for each uncertain variable;
- Sets of data on the system output are obtained by repeated model calculations;
- Statistical estimates are calculated from the data;
- Sensitivity analysis of input and output variables is performed.
In this work the stochastic analysis based on Monte Carlo simulation was carried out in a spreadsheet model created in MS Excel 2002 environment utilising @risk software.
STOCHASTIC SIMULATION METHODOLOGY
The proposed simulation method uses deterministic models without modification. In this work, models in a general-purpose process simulator, SuperPro DesignerTM v. 3.0, were directly used.
The first step of stochastic simulation is to determine the range and distribution of the uncertain variables. This step consists of the following procedures.
- Basic assessment of uncertainties of the process;
- Selection of uncertain variables;
- Gathering information for selected variables;
- Estimation of uncertainties based on available information;
Various probability distributions can be used to represent uncertainties of the variables. Selection of a probability function for an uncertain variable depends on the characteristics of the variables and the amount of variable information on the uncertainties of the variable. The most frequently distribution function are uniform distribution, normal distribution, and triangular distribution. Uniform distribution is need when information is poor and only the limiting values are known. As it has no central tendency, the uncertainties result in broad distribution of the values of the output variables. Normal distribution is known as a widely applicable distribution in statistics. Triangular distribution is used when he central and limiting values are known.
In this work uniform distribution was used based on factorial experimental planning techniques (PANNIR e al, 1998). With these experiments was carried out eight simulation utilising SuperPro Designer. The Table 1. shows the factorial experimental planning utilised.
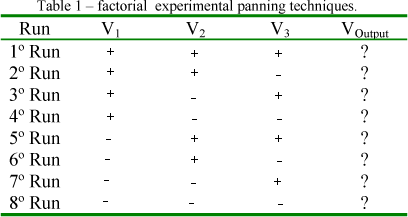
V is an input variable or parameter and the plus codification represent the maximum value and the minus codification represent minimum value assumed for the variable or parameters.
After carrying out the set of simulation proposed in the Table 1, the second step is to conduct a regression analysis to determine a model which is the best fit to the range of input parameters and variables, and output variables. In the present study the equation 1 was used. The regression analysis is the most important step in order to integrate the deterministic flowsheet model to the spreadsheet model.
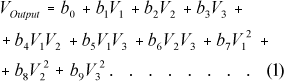
Where,
b0, b1, ... b9 are regression parameters;
V1, V2 and V3 are independent variables;
VOutput is dependent variable.
The third step is to generate samples according to the selected probability distribution function
The fourth step is the propagation of uncertainties through the model. This step comprises samples allocation to the model input, model calculation, and storage of the calculation results.
Finally, the fifth step is the uncertainty analysis of the simulation results. Uncertainties of the output variables are represented by moments of distribution. The distribution of the output variables can be described by various uncertainty displays such as cumulative distribution function, probability density function, box plot, bar graph, etc. The figure 1 shows the basic operation of the stochastic simulation method.
CASE STUDY
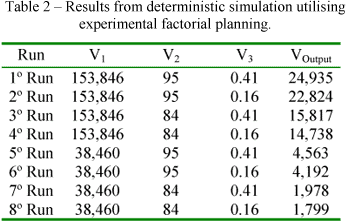
Based on data obtained in each step of ethanol process production and, physical and thermodynamic properties of the input and output stream simulations was carried out for Brazilian medium scale distillery with conventional process and the performance and applicability of the developed stochastic simulation methodology was tested. The figure 2 shows the simplified schematic of the conventional process of the fuel ethanol production from sugar cane (JOSHI and PANDEY, 1999). The objective is to conduct an economical risk analysis evaluation due of the effect of uncertainties of the input variables. The simulated situation is to predict the behaviour of the annual profit (VOutput) based on change of the distribution of feed flow rate (V1), yield of fermentation (V2) and selling price (V3), base on uniform distribution with minimum 38,460 kg/h and maximum 153,846 kg/h, minimum 84% and maximum 95%, minimum 0.16 R$ and 0.41 R$, respectively. This experimental factorial planning is illustrated in the table 2 represented in the columns 2, 3 and 4.
Base on simplified process flow diagram of fuel ethanol production proposed by (JOSHI and PANDEY, 1999) out lined in the figure 2 the deterministic simulation using SuperPro DesigneTM v. 3.0 software has been carried out. Where,
- First utilising the software databank, the components used in the process was defined;
- The equipment required was selected and Draw out the flowsheet (Figure 3.);
- The input streams and process parameters information have been specified;
- After the conduct the three steps above, the process simulation was conducted and the mass Balance, energy balance and output streams information was automatically solved;
- Now, with the changing of the stochastic parameters based on the experimental factorial planning out lined in the table 2 the eight simulations runs proposed was take placed, the table 2 in the columns 5 shows the economical result;
- Finally, costs, mass and energy balances reporters, equipment sizing, output flow streams and composition, and final process flowsheet have been obtained.
Where,
V1: feed flow rate, (103)kg/h;
V2: yield fermentation, %;
V3: selling price, R$;
VOutput: annual net profit, R$.
Based on data eight data point from table 2 was determined the set of regression parameters which better fit to the equation 1. The table 3 shows results from non-linear regression analysis.

Based on the Monte Carlo method and statistical distribution of the input variables a spreadsheet model was developed using @Risk v. 5.0 software and the uncertainties were propagated through the model obtained from regression analysis utilising Statistics v. 5.0 software. In this case study, ten thousand simulation runs were carried out and for each groups sampling was realised one hundred iteration runs.
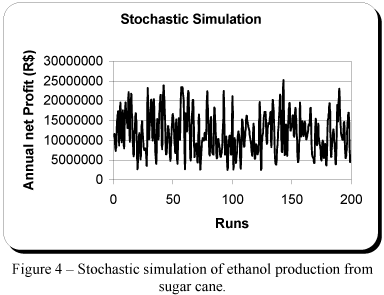
The analysis of the results show that the simulation was successful indicating the extent of uncertainties of the output variable with in tolerable limits of real values as shown the first two hundred simulations runs in the figure 4 and the trend of the change in these uncertainties using normal distribution was also identified. The nature of the output variable studied was observed and their probabilistic distribution are listed in the table 4.

CONCLUSIONS
- A methodology for stochastic analysis, using statistical properties of process variables and parameters, is presented. A case study of an industrial chemical process application was conducted successfully and analysed. The conclusions are summarised as follows.
- Conventional simulators do not take into account the uncertainties of the real process. Thus, there is no way to investigate the effect of the uncertainties in this chemical process simulation;
- The uncertainties analysis based on stochastic simulation have been discussed in this work using a model to integrate both deterministic and stochastic simulation. This model is implemented for fuel ethanol production.
- In stochastic analysis, the distribution used in Monte Carlo simulation is derived from input variables and parameters, therefore, the results depend only on process behaviour instead of the subjective judgement;
- The results of the case studies indicate that stochastic simulation is a powerful tool to evaluate the behaviour of the fuel ethanol production which has various changing uncertainties for several variables;
- The proposed method can be effectively extended to treat uncertainties of fuel ethanol process in small, medium end large scale of production;
- This simulation work developed in the present study can predict the probability of the viability of the fuel ethanol process from Brazilian biomass and its survive with different level of fuel ethanol selling price.
ACKNOWLEDGMENTS
The authors would like to thanks from CNPq/PIBIC, PPGEQ/DEQ/CT/UFRN and ANP/PRH - 14 for the financial support and laboratories facilities.
REFERENCES
[1]CHANG, C. P.; Lin, Z. S.; Stochastic Analysis of Decline Data for Production Prediction and Reserves Estimation, Journal of Petroleum Science and Engineering, v. 23, p. 149 - 160, 1999.
[2]DIWEKAR, U.M.; RUBIN, E.S. Stochastic Modelling of Chemical Processes, Computers Chem. Engng, v. 15, No. 2, p. 105 - 114, 1991.
[3]INTELLIGEN, INC.; Bio Pro Designer: An Advanced Computing Environment for Modelling and design of Integrated Biochemical Process, Computers Chem. Engng, v. 18, Suppl, p. S621 - S625, 1994
[4]INTELLIGEN, INC.; Users Guide's for the Pro-Designer (BioPro, EnviroPro, and SuperPro Designer) Family of Simulation and Designer Tools for the Process and Environment Industries, Intelligen Inc., Scott Plains, NJ, 1998.
[5]JOSHI, V. K.; PANDEY, A.; Biotechnology: Food Fermentation, Vol. II: Applied, Educational Publishers & Distributors, New Delhi - India, p. 1201 - 1230, 1999.
[6]LEE, K. L.; LEE, K. J.; CHOI, S. H.; YOON, E. S. Stochastic Dynamic Simulation of Chemical Process with Changing Uncertainties, Computers Chem. Engng, v. 20, Suppl, p. S557 - S562, 1996.
[7]MARQUARDT, W. Trends in Computer-Aided Process Modelling, Computers Chem. Engng, v. 20, No. 6/7, p. 591-609, 1996.
[8]MIZUTANI, F. T.; COSTA, A. L. H.; PESSOA, F. L. P. Stochastic Simulation of supercritical Fluid Extraction Processes, Braz. J. Chem. Eng, v. 17, No. 3, 2000.
[9]PANNIR P. V.; WOLF, D. M. B.; MELO, H.N.S. Process, Cost Modelling and Simulation for Integrated Project Development of Biomass for Fuel and rotein, J. Scien. Indus. Res., v.57, p. 567-574, 1998.
1 Author to whom correspondence should be addressed.










 How to cite this paper
How to cite this paper