An. 4. Enc. Energ. Meio Rural 2002
Modelos de estimativa da radiação difusa diária em Cascavel
Reinaldo Prandini RecieriI; Karina KoehlerII; Ana Caroline KoehlerII; Samuel Nelson Melegari de SouzaI
IProfessor Doutor do Curso de Engenharia Elétrica. FAG - Faculdade Assis Gurgacz reinaldo@fag.edu.br
IIAlunas do Curso de Engenharia Elétrica da FAG - Faculdade Assis Gurgacz
RESUMO
O presente trabalho, avalia-se vários modelos que correlacionam a fração da radiação difusa (Kd) com o índice de claridade (Kt) por meio de regressão polinomial e transcendental. O experimento foi conduzido na ESTAÇÃO EXPERIMENTAL de Cascavel (lat 24053'Sul, long 53023'Oeste, alt. 682m) no período de 1 de janeiro de 2001 a 31 de dezembro 2001. As componentes da radiação solar foram monitoradas por um piranômetro da KIPP&ZONEN (modelo - CM3) com constante de calibração 18,99 μV/Wm-2, um pireliômetro (NIP) da EPPLEY acoplado num rastreador solar modelo ST1. Na aquisição dos dados, utilizou-se um "micrologger" da CAMPBELL SCIENTIFIC-INC modelo CR10X, programado na freqüência de 1Hz e armazenar médias de 5 minutos. A distribuição dos valores diários (Kd x Kt), relacionados através de regressão polinomial e transcendental, forneceu equações de estimativa com elevados coeficientes de determinação. Dentre as correlações do modelo polinomial, os ajustes segundo os parâmetros RMSE e BEM, foram melhores na seqüência: 4º, 3º, 2º e 1º grau, respectivamente. A correlação do 4º grau, obtida para o local, indica que pode ser utilizada em outros locais de condições climáticas diferentes. A correlação do 4º grau: Kd=1,172-1,001Kt+3,992Kt2-11,742K t3+7,698Kt4 obtida para o local, generaliza a utilização da equação para estimar a radiação difusa para vários outros locais de condições climáticas diferentes.
Palavras chaves: radiação solar difusa; modelos de estimativa; índice de claridade.
ABSTRACT
In this work we evaluate, by means of polynomial and transcendental regression analysis, several models that relate the diffuse fraction of the global radiation (Kd) with the clearness index (Kt). The experiment was conducted in the Solar Radiometry Station of Cascavel/Pr from the first of January to the 31st of December, in the year of 2001. The solar radiation components were monitored by the following manufactured instruments: Pyranometer (KIPP&ZONEN (CM3) and pirheliometer (EPPLEY NIP) connected in a sun tracker (ST-1 model). A datalogger CR10X from the CAMPBELL SCIENTIFIC Inc. was used in the data acquisition. This datalogger was programmed in the frequency of 1 Hz storing an average of 5 minutes of collected data. The distribution of daily values for the relation Kd X Kt, find by regression analysis, provided equations with right values of determination coefficients. Among the polynomial equations the best values of RMSE an MBE were find in the 4th, 3rd, 2nd and 1st degrees, respectively. We also find that the 4th degree polynomial equation ( Kd=1,172-1,001Kt+3,992Kt2-11,742K t3+7,698Kt4) generalizes the utilization of equations for diffuse solar radiation estimation. This means that this equation probably can be applied for any place and climatic conditions.
INTRODUÇÃO
O conhecimento do comportamento da radiação difusa é de grande importância para áreas de ciências térmicas e agrária, visto que permitem a elaboração de projetos otimizados quanto ao aproveitamento da energia solar em edifícios e casas de vegetação que estão diretamente interligados as propriedades física e fisiológica de culturas. A dificuldade existente atualmente na caracterização desta componente solar, encontra-se no custo elevado dos radiômetros solares envolvidos nos métodos de medida: direto ou indireto, pois necessitam de dispositivos que acompanham o movimento relativo do sol.
Devido às dificuldades instrumentais, outra linha importante de estudos com radiação difusa é a dos modelos de estimativas. Neste, a radiação difusa é correlacionada com outro tipo de radiação, ou com um parâmetro meteorológico, por exemplo, a radiação global e a insolação relativa que são mais facilmente medido. Os modelos possuem menor precisão comparados aos métodos de medida, mas mostram ser úteis em locais que não possuem detectores solares disponíveis. O trabalho pioneiro, com modelos de estimativa entre irradiações global e difusa para um determinado local, foi elaborado por Liu & Jordan (1960), que relacionaram a razão das irradiações, difusa na superfície terrestre (Rd) e do topo da atmosfera (Ro) ou K'd=Rd/Ro , com a razão das irradiações, global na superfície terrestre (RG) e topo da atmosfera (Ro), também denominado de índice de claridade Kt (Kt=RG/Ro), para diversas situações de partições de tempo: horária, diária e mensal. Outra expressão utilizada é a razão entre as irradiações difusa e global na superfície terrestre (Rd/RG), que foi representada pelo símbolo Kd, pela razão Kt = RG/Ro. As duas curvas características apresentadas por Liu e Jordan foram, posteriormente, equacionadas por outros pesquisadores como: Klein (1976), que encontrou uma expressão estatística polinomial de 3º grau:
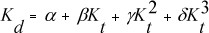
enquanto Bruno (1978) obteve:
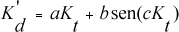
onde as constantes α, β, γ, δ, a, b e c são constantes determinadas estatisticamente através de regressão. Dos modelos, o tipo polinomial é o mais freqüentemente estudado, visto que, a correlação pode ser melhor ajustado em função do grau do polinômio, para locais com diferentes partições de tempo das irradiações.
A partir de 1960, diversos autores confirmaram a validade do modelo proposto para uma localidade porém, constataram que a correlação encontrada não poderia ser aplicada para regiões de grandes dimensões em toda sua extensão, não só devido a variabilidade climática da atmosfera, como também devido a latitude, como mostra o trabalho de Soler (1990).
Em função desta característica, vários modelos foram propostos com finalidade geográficas, que apesar de não serem muito precisos, podem ser utilizados quando não se tem informações da radiação na região. Exemplos deste tipo de modelo são os trabalhos publicados por : Collares-Pereira & Rabl (1979) e Erbs et al. (1982) para os Estados Unidos; Choudhury (1963) e Muneer & Hawas (1984) para a Índia; Ruth & Chant (1976), Tuller (1976) e Iqbal (1979a) para o Canada; Stanhill (1966) para Isrrael; Bartoli et al. (1982) para a Itália e Hantoria et al. (1997) para Espanha, entre muitos outros.
Outra fonte de variação nos estudos com modelagem da irradiação difusa é a partição das irradiações. Normalmente, as irradiações global, difusa e no topo da atmosfera são representadas pela partição horária, diária e média mensal, cuja escolha tende aos objetivos e à área de aplicação. Erbs et al. (1982) selecionaram as três partições para seus estudos. Orgill & Hollands (1977), Bruno (1978), Bartoli et al. (1982), Spencer (1982), Reindl et al. (1990), Chandrasekaran & Kumar (1994) e Srivastava et al. (1995), entre outros, optaram pela partição horária. Liu & Jordan (1960), Hontoria et al. (1997), Colares-Pereira & Rabl (1979), Lebaron & Dirmhirn (1983), Bartoli et al. (1982), Aragón et al. (1996), utilizaram partição diária. Com partição de média mensal, que exige banco de dados de vários anos de medidas, encontram-se trabalhos na literatura, em menor quantidade, tais como: Tuller (1976), Page (1961), Ma & Iqbal (1984), Iqbal (1978), Iqbal (1979 a e b) e Hay (1979), entre outros.
As correlações propostas na grande maioria dos trabalhos citados apresentaram grande variabilidade em função da partição utilizada e local estudado. Alguns preferem a dependência linear, outros de 3º ou 4º grau, cuja escolha depende do coeficiente de determinação ou parâmetros estatísticos de RMSE e MBE. Outros pesquisadores, ao invés de representar Kd=f(Kt) como uma única correlação, fazem opção por uma combinação de equações, em função de intervalos específicos de Kt.
No Brasil, o estudo com modelagem da radiação difusa é recente, pois poucos grupos tem o privilégio de estarem medindo de rotina esta componente, por qualquer um dos métodos recomendados em literatura. Dentre os locais, podem ser citados os grupos de radiação solar de Viçosa, IAG-USP/SP., Santa Catarina e UNESP de Botucatu. Os resultados iniciais foram divulgados pelos grupos de Viçosa e Botucatu, através dos trabalhos: Souza & Alves (1994); Lima et al. (1995) e Ricieri et al. (1996).
Face a estas realidades, o presente trabalho tem como objetivo em propor um modelo local com partição diária de estimativa da radiação difusa.
MATERIAL E MÉTODOS
O experimento foi realizado na ESTAÇÃO EXPERIMENTAL AGROMETEOROLÓGICA de Cascavel (latitude 24053'Sul, longitude 43023'Oeste, altitude 682m), no período de 1 de janeiro de 2001 à 31 de dezembro de 2001.
A densidade de fluxo global (IG) foi obtida através de um piranômetro KIPP&ZONEN Modelo - CM3, com constante de calibração igual a 18,99μV/Wm-2, posicionado num plano horizontal.
Na medida da densidade de fluxo direto na incidência normal (IDN), foi utilizado um pireliômetro EPPLEY-NIP, com fator de calibração igual a 8,40μV/Wm-2, acoplado a um rastreador solar EPPLEY modelo ST-1.
A densidade de fluxo da radiação difusa (Id) foi obtida pela diferença entre as densidades de fluxo global (IG) e direta de incidência normal (IDN) projetada na horizontal, através da equação: Id=IG-IDNCosz.
Foi utilizado uma aquisição de dados "micrologger" da CAMPBELL SCIENTIFIC-INC modelo CR10X, programado para realizar uma leitura por segundo de cada canal e armazenar a média aritmética de cinco minutos.
Elaborou-se um programa em linguagem BASIC, com equações citadas por Iqbal (1983), para calcular na mesma frequência da aquisição dos dados experimentais, o ângulo horário do nascer do Sol (ws), a declinação solar (δ), irradiância solar no topo da atmosfera (Ro), cosseno do ângulo zenital (cosz).
RESULTADOS E DISCUSSÃO
A Figura (1) mostra a distribuição diária de Kd em função de Kt. Independentemente da partição das irradiações global e difusa, a distribuição característica obtida é similar às apresentadas por outros pesquisadores. Nos limites, quando Kt tende a zero, Kd tende a um, e quando Kd tende a zero, Kt tende a um. No intervalo intermediário, Kt pode assumir tendência linear, polinomial, de 2ª, 3ª ou 4ª ordem, ou mesmo uma exponencial.
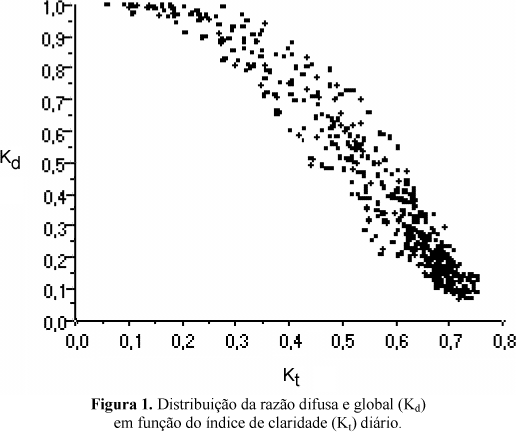
Submetendo a distribuição dos pontos experimentais (Kd x Kt) a programas estatísticos de regressões do tipo polinomial e transcedental, obteve-se os seguintes modelos empíricos para calcular a radiação difusa local.
MODELO POLINOMIAL
a) Correlação linear. A Figura (2) mostra o ajuste da correlação linear à distribuição dos dados para Cascavel, bem como de vários pesquisadores que propuseram equações do tipo linear em outras localidades.
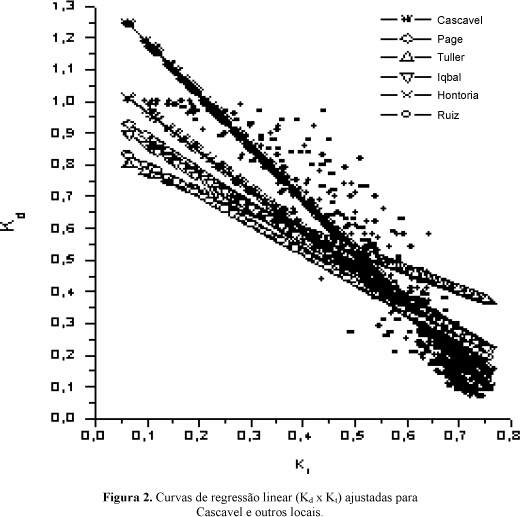
A equação obtida com o respectivo coeficiente de determinação R2 foi:
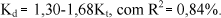
O coeficiente de determinação R2 próximo de 90% indica que Kd pode ser estimado a partir de Kt com razoável nível de precisão. O modelo linear é similar às correlações médias mensais obtidas por:
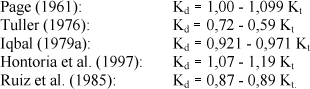
A diferenciação das equações estão nos coeficientes de intercepto e coeficiente angular. O coeficiente de intercepto maior que 1 estabelece um limite para a utilização de Kt, uma vez que fisicamente na superfície terrestre, a irradiação difusa não pode ser maior que a irradiação global. Para a correlação linear obtida em Cascavel e a de Hontoria, as equações somente terão validades para valores de Kt superiores a 0,2 e 0,05, respectivamente.
O coeficiente angular, que representa efetivamente a capacidade de difusão de luz solar da atmosfera, depende das condições climáticas e do local. Uma comparação entre as seis equações mostra que, a menos do modelo de Tuller, o modelo proposto tende a superestimar o valor de Kd para valores de Kt em torno de até 0,58, e subestimar, para valores de Kt de 0,58 a 0,73, aproximadamente.
Comparando os modelos citados através da raiz quadrada do erro quadrático médio (RMSE) que está associado a dispersão de dados e do erro médio (MBE), que está associado com tendência de dispersão dos pontos em relação à equação média, definidos através das relações:
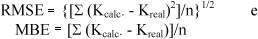
tem-se os dois parâmetros estatísticos apresentados no Quadro (1).
b) Correlação parabólica. A Figura (3) mostra a curva ajustada por regressão polinomial de 2º grau à distribuição Kd = f(Kt).
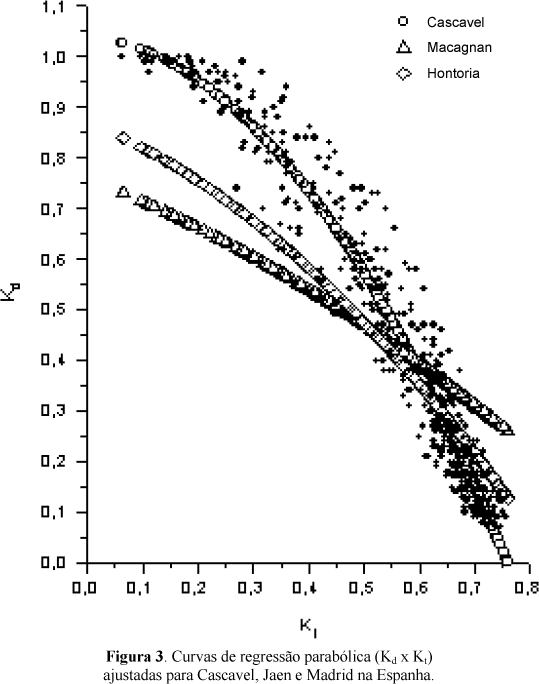
A equação obtida com o coeficiente de determinação foi:
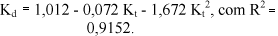
O coeficiente de determinação R2 = 91,52% indica melhor ajuste ao obtido no modelo linear. Resultados similares com correlação parabólica foram obtidos recentemente para cidades de Madrid e Jaen, na Espanha, por:
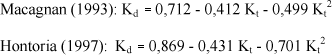
Apesar da similaridade de comportamento, o distanciamento entre as curvas mostra que o modelo parabólico é dependente das condições climáticas e do local. O Quadro (2) mostra os resultados estatísticos do ajuste parabólico que, no caso de Cascavel, quando relacionados aos resultados obtidos no modelo linear, indicam uma melhoria no valor do parâmetro RMSE, próximo de 8,0%.
A equação proposta por Hontoria apresenta melhor ajuste que a de Macagnan cujos RMSE obtidos foram da ordem de 13,37% e 18,72%, respectivamente. O erro médio estatístico MBE para os três casos analisados mostra valores negativos e, portanto, indicam que, se as mesmas fossem utilizadas em Cascavel, os valores de Kd calculados seriam subestimados em relação aos valores reais.
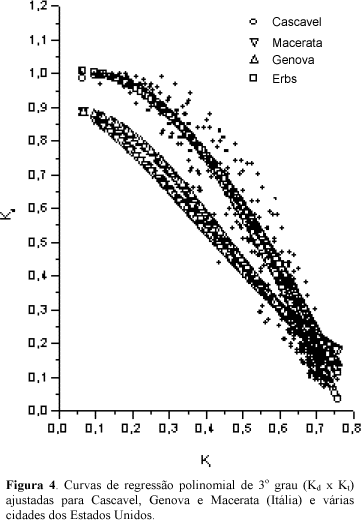
c) Correlação polinomial do 3º grau. A Figura (4) mostra a curva polinomial de 3º grau ajustada aos dados experimentais e curvas de vários outros pesquisadores como Erbs (1982) e Bartoli et al. (1982) (Macerata e Genova).
A equação obtida para Cascavel:
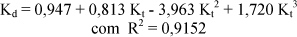
Em função do coeficiente de determinação R2 = 91,52%, estatisticamente não ocorreu uma melhoria significativa entre os ajustes das equações de 2º e 3º grau, que praticamente foram iguais. Numericamente, o resultado pode ser considerado bom, visto que a equação estima com elevado nível de probabilidade.
Comparando a equação obtida para Cascavel com as equações de correlações divulgadas por Bartoli e Erbs entre outros que trabalharam com equações polinomiais de 3ª ordem, notamos que a similaridade ocorre apenas no grau polinomial e difere nos sinais das constantes das funções. Algumas correlações Kd = f(Kt) de 3º grau citadas na literatura são:
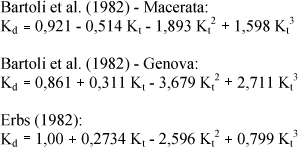
Graficamente, é possível observar através das curvas que a correlação polinomial de terceiro grau, a exemplo da equação do 2º grau, também não é ajustável para todos os locais. O modelo para quatro cidades dos EEUU obtido por Erbs et al. (1982) se aproxima de Cascavel, porém difere significativamente em relação às cidades de Genova e Macerata (Bartoli et al., 1982), que subestimam os níveis de irradiação difusa para o local. No Quadro (3) estão representados os parâmetros estatísticos RMSE e MBE para as equações do 3º grau.
Do ponto de vista comparativo dos parâmetros estatísticos RMSE e MBE, o modelo polinomial de 3º grau apresenta, para Cascavel, um valor estatisticamente igual ao de 2º grau, com diferença no sinal de MBE que é positivo; portanto, o modelo tende a superestimar a irradiação difusa. O modelo de ERBS apresenta valores para RMSE e MBE igual a 9,3%, aproximadamente. O modelo polinomial de 3º grau de Bartoli, que se aplica com elevada precisão para as cidades de Genova e Macerata, subestima o nível de irradiação difusa em Cascavel, com um RMSE na faixa de 13% e 15%, respectivamente.
d) Equação polinomial do 4º grau. A Figura (5) mostra a curva polinomial de 4º grau ajustada à distribuição de dados de Cascavel e de outros locais.
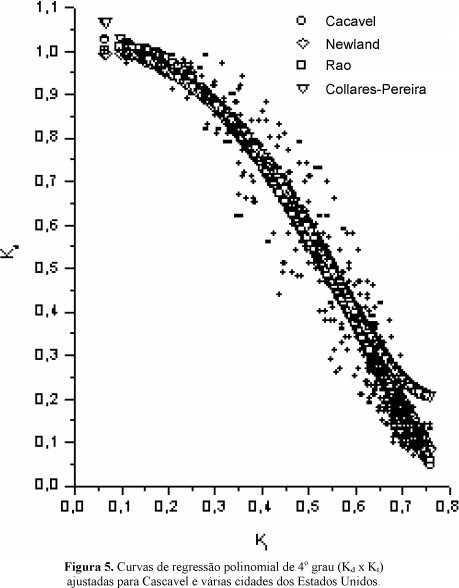
A equação obtida foi:
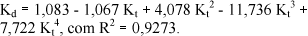
A correlação polinomial de quarto grau não melhora o coeficiente de determinação em relação ao de 3º grau e 2º grau, no entanto, generaliza a estimativa da radiação para vários locais, não importando as condições climáticas, como mostram os modelos obtidos por Collares-Pereira & Rabl (1979) para cinco cidades dos Estados Unidos; Newland (1989) para Macau; Rao et al. (1984) para Corvallis\Oregon entre outros, que obtiveram as equações:
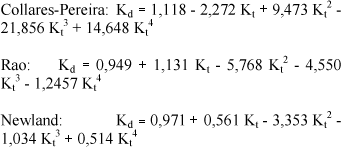
Para o intervalo de Kt entre 0,15 e 6,5, as curvas estão muito próximas à obtida em Cascavel. Uma restrição apenas para valores acima de 0,65 na equação de Collares-Pereira, que tende a um valor constante a partir de Kt acima de 0,65. O ajuste das equações na distribuição dos dados pode ser melhor observada no Quadro (4) que expressa os valores RMSE e MBE para todos os modelos.
Através dos valores apresentados no Quadro (4) de RMSE, observamos que os modelos de Cascavel, Newland e Rao encontram-se muito próximos estatisticamente e, em torno de 8,0% e 9,6% para o modelo de Collares-Pereira e Rabl. A diferença deste último para os demais deve ser devido aos valores de Kt inferiores a 0,15 e superiores a 0,65, que superestimam os valores de Kd em relação aos outros três modelos. Os valores de MBE mostram que a correlação proposta superestima a irradiação difusa, enquanto as demais subestimam.
Comparando os valores determinados de RMSE neste trabalho com valores citados na literatura, como mostram os trabalhos: Hontoria (1997): RMSE = 9,14%; Macagnan (1993): RMSE = 10,45%; Collares-Pereira & Rabl (1979): RMSE = 14,79%; Ruiz (1985): RMSE = 11,18%; Orgill & Hollands (1977): RMSE = 14,2%; Erbs et al. (1982): RMSE = 14,0%; Reindl et al. (1990): RMSE = 13,7%; Gariepys (1980): RMSE = 9,6%; Hay (1979): RMSE = 11,4%; Rietveld (1978): RMSE = 15,8%; Bartoli et al. (1982): RMSE = 10,0%, entre muitos outros, independentemente da partição e do tipo do grau da regressão polinomial, os resultados obtidos a partir da equação de 2º grau podem ser considerados bons, podendo ser utilizados para o local com uma imprecisão na faixa de 8,0%.
MODELO TRANSCENDENTAL
Na tentativa de uma melhoria de correlação, considerando a distribuição característica entre Kd e Kt, os dados experimentais foram submetidos ao modelo transcendental do tipo exponencial, similar ao modelo de Bartoli et al. (1982), expresso por:
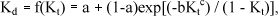
onde a, b e c são constantes ajustáveis da equação de regressão.
A figura (6) mostra a curva de regressão transcendental à distribuição de Cascavel e também as curvas geradas pelo modelo transcendental de Bartoli et al. (1982) para as cidades de Genova e Macerata, respectivamente.
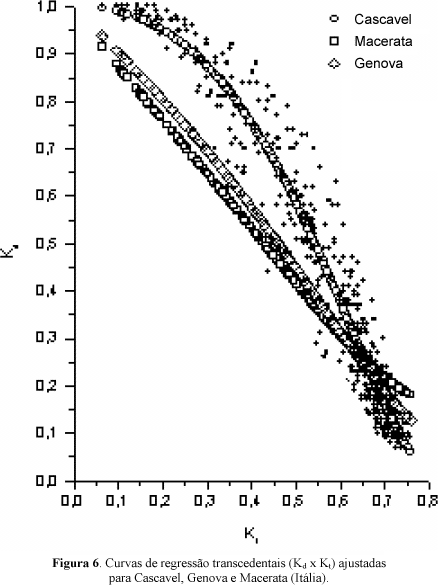
A equação transcendental obtida para Cascavel com seu respectivo RMSE foi:
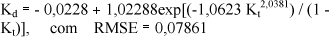
O resultado mostra que a irradiação difusa pode ser estimada com um nível de precisão próximo de 8,0% e de forma similar às equações de estimativa polinomiais de 2ª, 3ª e 4ª ordem.
As equações para as duas cidades da Itália foram:
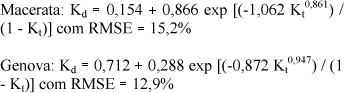
Os valores numéricos do RMSE das 3 equações mostram que o modelo transcendental proposto por Bartoli é dependente do local e das condições climáticas. A utilização de qualquer uma das equações propostas se aplicaria à Cascavel com diferenças de 7% e 5% em relação ao modelo local.
CONCLUSÕES
Diante dos resultados obtidos, podemos concluir que:
• a curva de distribuição experimental da razão difusa pela global (Kd) em função do índice de claridade (Kt), obtida para Cascavel, com partição diária, apresentou característica similar às apresentadas na literatura, independentemente do clima, local e partição;
• nos modelos de regressão obtidos com a distribuição dos dados (Kd x Kt) locais, não constatou-se melhoria no ajuste entre as correlações de 3º e 4º grau do modelo polinomial e o modelo transcendental;
• dentre as correlações do modelo polinomial, segundo os parâmetros estatísticos RMSE e MBE, os melhores ajustes foram obtidos nos modelos de 4º, 3º e 2º grau, respectivamente, com seus valores muito próximos;
• a correlação do 4º grau do modelo polinomial universaliza o uso da equação de estimativa da radiação difusa para vários locais com condições climáticas diferentes.
REFERÊNCIAS BIBLIOGRÁFICAS
[ 1 ] LIU, B.Y.H., JORDAN, R.C. The interrelationship and characteristic distribution of direta, difuse and total solar radiation. Solar Energy, v.4, p.1-19, 1960.
[ 2 ] BRUNO, R. A correction procedure for separating direct and diffuse insolation on a horizontal surface. Solar Energy, v.20, p.97-100, 1978.
[ 3 ] SOLER, A. Dependence on latitude of the relation between the diffuse fraction of solar radiation and the ratio of global to - extraterrestrial radiation for monthly average daily values. Solar Energy, v.44, n.5, p.297-302, 1990.
[ 4 ] ERBS, D.G., KLEIN, S.A., DUFFIE, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthy-average global radiation. Solar Energy, v.28, p.293-302, 1982.
[ 5 ] CHOUDHURY, N.K.D. Solar radiation at New Delhi. Solar Energy, v.7, n.2, p.44-52, 1963.
[ 6 ] CHANDRASEKARAN, S., KUMAR, S. Hourly diffuse fraction correlation at a tropical location. Solar Energy, v.53, n.6, p.505-510, 1994.
[ 7 ] MUNEER, T., HAWAS, M.M. Correlation between daily diffuse and global radiation for India. Energy Conversion Management, v.24, n.2, p.151-154, 1984.
[ 8 ] RUIZ, F.F., GUTIÉRREZ, J., BENET, G., ANDRÉS, J.M. Correlation between diffuse and global solar radiation for various sites in Spain. In: CONGRESO COMPLÉS , 23, 1985. p.97-110.
[ 9 ] IQBAL, M. A study of Canadian diffuse and total solar radiation data - I, Monthly average daily horizontal radiation. Solar Energy, v.1, p.81-86, 1979a.
[ 10 ] STANHILL, G. Diffuse skin and cloud radiation in Israel. Solar Energy, v.10,n.2, p.96-101, 1966.
[ 11 ] BARTOLI, B., CLUOMO, V., AMATO, U., BARONE, G., MATTARELLI, P. Diffuse and beam components of daily global radiation in Genova and Macerata. Solar Energy, v.28, p.307-311, 1982.
[ 12 ] ORGILL, J.F., HOLLANDS, K.G.T. Correlation equation for hourly diffuse radiation on a horizontal surface. Solar Energy, v.19, p.357-359, 1977.
[ 13 ] HONTORIA, L., PÉREZ, P.J., ALMONACID, G. Estudio comparativo de diferentes correlaciones entre el índice de claridad y la fracción de difusa para diferentes localizaciones. In: CONGRESSO IBÉRICO DE ENERGIA, 8, 1997, Porto, Energia solar e qualidade de vida, 1997. p.103-110.
[ 14 ] SPENCER, J.W. A comparison of methods for estimating hourly diffuse solar radiation from global solar radiation. Solar Energy, v.29, n.1, p.19-32, 1982.
[ 15 ] REINDL, D.T., BECKMAN, W.A., DIFFIE, J.A. Diffuse fraction correlations. Solar Energy, v.45, n.1, 1990.
[ 16 ] TULLER, S.E. The relationship between diffuse, total and extraterrestrial solar radiation. Solar Energy, v.3, p.259-263, 1976.
[ 17 ] SRIVASTAVA, S.K., GAUR, A., SINGH, O.P., TIWARI, R.N. Comparison of methods for estimating daily and hourly diffuse solar radiation. Applied Energy, v.51, p.119-123, 1995.
[ 18 ] COLLARES-PEREIRA, M., RABL, A. The average distribution of solar radiation - correlations between diffuse and hemispherical and between daily and hourly insolation values. Solar Energy, v.22, p.155-164, 1979.
[ 19 ] LEBARON, B.A., PETERSON, W.A., DIRMHIRN I. Correlations for diffuse irradiance measured with shadonbands. Solar Energy, v.25, p.1-17, 1980.
[ 20] ARAGÓN, D.F. GONZÁLES, M., GUSMÁM, M., QUIROGA, Z., SIMBAQUEVA, F.O. Relacion entre la radiación solar difusa y radiación solar global en una localidad Colombiana. Cenicafé, v.47, n.3, p.159-166, 1996.
[ 21 ] PAGE, J.K. The estimation of monthly mean values of daily total short wave radiation on vertical and inclined surfaces from sunshine records for latitudes 40ºN-40ºS. Proc. U.N. Conf. on New Sources of Energy, v.4, p.378-390, 1961.
[ 22 ] MA., C.C.Y., IQBAL, M. Statistical comparison of solar radiation correlations. Solar Energy, v.33, n.2, p.143-148, 1984.
[ 23 ] IQBAL, M. A study of Canadian diffuse and total solar radiation data - II, Monthly average hourly horizontal radiation. Solar Energy, v.22, p.87-90, 1979b.
[ 24 ] HAY, J.E. Cauculation of monthly mean solar radiation for horizontal and inclined surfaces. Solar Energy, v.33, n.4, p.301-307, 1979.
[ 25 ] SOUZA, M.J.H., ALVES, A.R. Avaliação de métodos para a estimação de irradiância solar direta em Viçosa-MG. In: CONGRESSO BRASILEIRO DE METEOROLOGIA, VII, 1994, Belo Horizonte, A meteorologia na prevenção dos desastres naturais. Rio de Janeiro: Sociedade Brasileira de meteorologia, 1994. p.362-365.
[ 26 ] LIMA, F.Z., ALVES, A.R., MARTINS, J.H., COSTA, J.M.N. Desenvolvimento de modelos para estimação da irradiaância solar difusa horária. In: CONGRESSO BRASILEIRO DE ENGENHARIA AGRÍCOLA, XXIV, 1995, Viçosa-MG., 1995, p.20-25.
[ 27 ] RICIERI, R.P., ESCOBEDO, J.F., MARTINS, D. Relações da radiações solar difusa em Botucatu. In: CONGRESSO BRASILEIRO DE METEOROLOGIA, IX, 1996, Campos do Jordão, Os benefícios das modernas técnicas de previsão de tempo e clima para as atividades sócio-econômicas. Rio de Janeiro: Sociedade Brasileira de meteorologia, 1996. p.547-550. Energy, v.3, p.259-263, 1976.
 Endereço para correspondência:
Endereço para correspondência:
Departamento de Engenharia, FAG
Faculdade Assis Gurgacz Avenida das Torres
500 Fone/Fax: (45)321-3900 CEP: 85800-000
Bairro FAG - Cascavel/PR










 How to cite this paper
How to cite this paper