Services
An. 5. Enc. Energ. Meio Rural 2004
Estudio cinético de la pirólisis de fangos mediante experimentos dinámicos
J. ArauzoI; A. GonzaloI; J.L. SánchezI; F.L.P. ResendeII; J.D. RochaIII, V; J.M. Mesa PérezIV, V
IGrupo de Procesos Termoquímicos, Instituto de Investigación en Ingeniería de Aragón (I3A), Universidad de Zaragoza, España
IIChemical Engineering Dept., University of Michigan, U.S.A.
IIINúcleo Interdisciplinar de Planejamento Energético, NIPE/UNICAMP, Campinas, SP, Brasil
IVFaculdade de Engenharia Agrícola, FEAGRI/UNICAMP
VBioware Tecnologia, www.bioware.com.br, Campinas, SP, Brasil
RESUMEN
En el presente trabajo se muestra un modelo que describe la cinética de la pirólisis de fangos de estaciones depuradoras (EDAR) basado en datos obtenidos de experimentos dinámicos realizados en una termobalanza, con velocidades de calentamiento de 5 a 20ºC/min en un rango de temperatura de 40 a 900ºC. Un modelo simple de orden uno o próximo a uno es capaz de predecir aceptablemente la conversión final alcanzada, sin embargo al observar la velocidad de pérdida de peso, un modelo simple no es capaz de simular los distintos máximos obtenidos en la velocidad. Tal y como se muestra, el mejor ajuste obtenido se ha logrado mediante un modelo que tiene en cuenta cuatro fracciones que se descomponen independientemente mediante una cinética de orden uno.
Palabras clave: Fangos de depuradora, pirólisis, termogravimetría, cinética.
ABSTRACT
In this work, a pyrolysis model is presented in order to describe the pyrolysis kinetics of sewage sludge. Data were obtained from dynamic experiments, at heating rates of 5 to 20 ºC/min and in a temperature range of 40 to 900ºC. A simple first order or near first order can predict reasonably well the final conversion reached, but, in what concerns the weight loss rate, a simple model cannot predict the peaks obtained in the weight loss rate. As it is shown, the best fit has been obtained by a model which takes into account four fractions which decompose independently following a first order kinetics.
1. Introducción
Los lodos activos, o fangos, constituyen un residuo generado en el tratamiento de aguas residuales de procedencia urbana o industrial. La tasa de generación de estos residuos está aumentando continuamente debido a legislaciones medioambientales cada vez más estrictas en cuanto a la calidad del agua que puede verterse a las aguas superficiales o marinas. Así por ejemplo en la Unión Europea se estima, sin tener en cuenta la reciente ampliación a 25 países, que para el año 2005 la producción de fango será de alrededor de 8-10 Mt/año.
Hasta la fecha, las vías principales de eliminación y/o gestión de lodos han sido las siguientes: aplicaciones en tierras de cultivo, deposición controlada en vertederos, incineración y vertido al mar. En la Figura 1 se muestra una estimación de la evolución de las distintas alternativas de gestión de los lodos para la UE hasta el 2005 ( Werther y Ogada 1999).
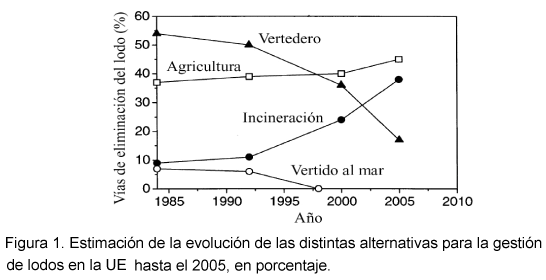
La aplicación en tierras de cultivo (agricultura) es, en España, la vía preferida, con la cual se pretende valorizar hasta el 70 % de los fangos generados para el año 2007. Sin embargo, tal y como se indica en la Directiva del Consejo de la UE 91/271/EEC de 21 Mayo de 1991 sobre tratamiento de aguas residuales urbanas puede llegar a ser una alternativa problemática debido a la acumulación de metales pesados y fosfatos. Por otro lado, la deposición controlada es la vía de gestión menos sostenible y debe considerarse como una solución final.
La pirólisis puede ser un proceso alternativo para la gestión y valorización de este residuo, ya que puede permitir la producción de gases y aceites de alto poder calorífico, disminuyendo la formación de dioxinas, NOx y SOx y concentrando los metales pesados en el residuo sólido (char) (Furness y cols. 2000, Inguanzo y cols. 2002, Caballero y cols. 1997, Conesa y cols. 1998).
La termogravimetría es una técnica comúnmente utilizada para estudiar las reacciones de descomposición de materiales sólidos, ya que puede proporcionar información sobre la composición del material, los parámetros cinéticos y los distintos procesos que tienen lugar en un rango determinado de temperatura. Mediante termogravimetría Urban y Antal (1982) obtuvieron las energías aparentes de activación para la degradación de fangos en dos etapas, una fracción orgánica (84 kJ/mol) y otra celulósica (209 kJ/mol). Un modelo diferente (Chen y Jeyaseelan, 2001) propone cuatro reacciones consecutivas en competición utilizado para simular la pirólisis de fango con y sin activación mediante adición de ZnCl2. He y cols. (2000, 2001) encontraron los siguientes parámetros para una reacción simple de descomposición: orden, n = 2, factor preexponencial, Z = 8.5 s-1 y energía de activación E = 37.9 kJ/mol. Al dividir la curva de descomposición en 4 partes, encontraron los siguientes parámetros Z1 = 4.15 x 106 s-1, n1 = 2, E1 = 98 kJ/mol; Z2 = 1.42 x 105 s-1, n2 = 2, E2 = 85 kJ/mol, Z3 = 1.01 x 1012 s-1, n3 = 4, E3 = 190 kJ/mol; y Z4 = 1.33 x 109 s-1, n4 = 4, E4 = 146 kJ/mol. En un trabajo anterior (Resende y cols. 2004a) se ha mostrado como, para un fango obtenido mediante digestión anaerobica y secado térmico, la pérdida de peso se puede simular mediante un reacción de orden 1.2 con una energía de activación de 45.3 kJ/mol y un factor preexponencial Z= 1.4 s-1, sin embargo, aunque el coeficiente regresión de la curva simulada frente a la experimental fue alto, de 0.983 para velocidades de calentamiento de 5 a 20 ºC/min, un modelo simple no puede simular las curvas de velocidad de conversión, o pérdida de peso, que presentan varios picos, por lo que puede ser de interés introducir un modelo más complejo que se ajuste con mayor precisión a las curvas observadas.
2. Método experimental
En la Tabla I se muestran los análisis inmediato y elemental del fango utilizado en este trabajo, junto con el poder calorífico superior (PCS) e inferior (PCI). Se puede observar el alto porcentaje de cenizas, próximo al 50%, que se puede achacar a que el fango fue digerido anaeróbicamente, lo que reduce la cantidad de materia orgánica presente.
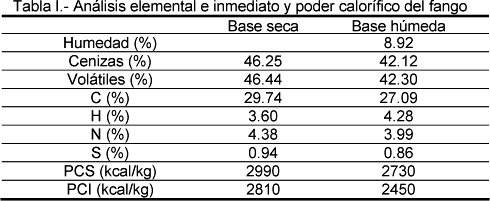
Los experimentos se han llevado a cabo en una termobalanza CAHN TG 131, en un rango de temperatura de 40 a 900 ºC y usando nitrógeno como gas inerte. Se realizaron experimentos previos para analizar la influencia de tamaño de partícula, caudal de gas inerte, masa inicial de muestra y velocidad de calentamiento sobre la conversión final alcanzada, de modo que se pueda asegurar que se trabaja sin restricciones de transferencia de materia y energía (Resende y cols. 2004b). Los experimentos se han realizado con las siguientes condiciones: diámetro de partícula +50 μm-106 μm, caudal de nitrógeno 100 cm3N/min, peso inicial de muestra 10 mg, velocidades de calentamiento (β): 5, 10, 15 y 20 ºC/min.
3. Resultados y modelo cinético
Para las reacciones de descomposición se suele suponer que la ecuación cinética es de la forma que se muestra en la ecuación 1:

donde f es la fracción en peso de muestra, k es la constante cinética (normalmente se supone que sigue la ecuación de Arrehenius) y F(f) es la función que determina la dependencia de la velocidad con f y debe ser determinada experimentalmente. Es bastante común suponer que la función F(f) toma la forma (f-f")n, siendo n el orden de la reacción y f" la fracción de peso final, aunque es posible encontrar muchas otras funciones en la bibliografía, como muestran Vlaev y cols. (2003) y Orfao y Martins (2002) por ejemplo.
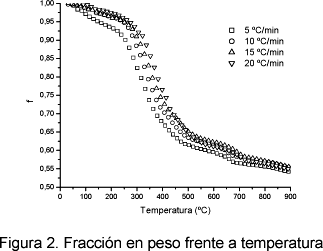
En la Figura 2 se muestra la fracción en peso de fango frente a la temperatura para las distintas β. Las curvas para las distintas velocidades de calentamiento tienen la misma forma, con un ligero desplazamiento debido a las distintas velocidades de calentamiento utilizadas.
En la figura 3 se muestra la derivada de la fracción en peso respecto a la temperatura.
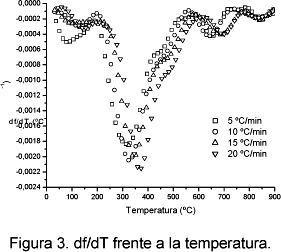
En las curvas mostradas en la Figura 3, se puede observar que, aunque la mayor parte de la descomposición ocurre entre 200 y 550 ºC, existen varios picos, que no pueden ser explicados con una descomposición simple, aunque, como se ha comprobado (Resende y cols. 2004a), los datos de conversión ajustan razonablemente bien con n=1.2. La existencia de varios picos en la derivada de la conversión se puede explicar mediante una serie de reacciones consecutivas o mediante reacciones independientes que ocurren en paralelo. Este último modelo se ha sido aplicado a materiales lignocelulósicos (Orfao y cols. 1999, Manya y cols. 2003), harinas cárnicas (Conesa y cols. 2003) y fangos (Conesa y cols. 1997).
Suponiendo un orden de reacción n=1 y que el fango se halla compuesto de N fracciones que se descomponen independientemente se puede escribir:
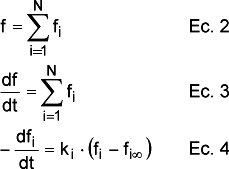
donde cada ki responde a la ecuación de Arrehenius y tiene su propio factor preexponencial Zi y energía de activación Ei. En la ecuación 4 es, obviamente, posible separar variables e integrar, siendo necesario conocer, o usar como parámetro de ajuste, fi,0 y fi". Como
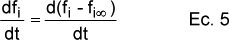
se puede agrupar (fi-fi") para utilizarlo como parámetro de ajuste, y teniendo en cuenta que
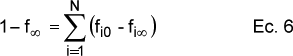
el número de parámetros que se utilizan son N factores preexponenciales Zi, N energías de activacion Ei y N-1 fracciones (fi0-fi").
Para realizar los cálculos se ha utilizado la derivada de f respecto a la temperatura, que se relaciona con la derivada respecto al tiempo mediante la velocidad de calentamiento de cada experimento:
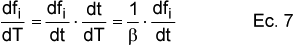
Aplicando las ecuaciones anteriores, separando variables e integrando entre la temperatura inicial T0 y una temperatura T, para cada una de las fracciones se puede calcular su evolución con la temperatura mediante la ecuación 8:
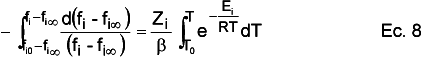
que resolviendo la integral para el término que depende de las fracciones queda como:
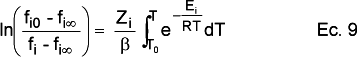
Hay que tener en cuenta que el término basado en la temperatura no tiene una solución analítica, y por tanto debe integrarse numéricamente o sustituirse por una función que se le aproxime.
Con el fin de determinar los parámetros que mejor ajustan los datos experimentales, para las cuatro velocidades de calentamiento simultáneamente, se ha integrado numéricamente el término derecho de la ecuación 9, tomando los datos experimentales de temperatura, aproximadamente unos 500 datos para cada curva experimental. El método numérico utilizado para la integración ha sido el método de Simpson 1/3, tomando 4 intervalos entre cada par de puntos experimentales de temperatura, lo que da unos 2000 intervalos para todo el rango de temperatura experimental. El error cometido en la integración numérica se puede considerar despreciable, ya que es proporcional a la cuarta derivada de la ecuación de Arrehenius, que para las energías de activación obtenidas es prácticamente cero. De este modo se puede calcular, para cada velocidad de calentamiento, los coeficientes de regresión lineal de las fracciones calculadas frente a las experimentales (fexperimental,β=fcalculada,β ) y de las derivadas (df/dTexperimental,β=df/dTcalculada,β ). Como función objetivo (F.O.), que debe ser máxima, para determinar los parámetros que mejor ajustan las curvas experimentales, tanto de f como de df/dT, se ha tomado el producto de los coeficientes de regresión lineal medios para las cuatro β utilizadas de f y df/dT:
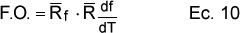
con
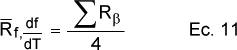
y Rβ el coeficiente de regresión lineal calculado para todos los puntos experimentales de f o df/dT frente a los calculados con el modelo.
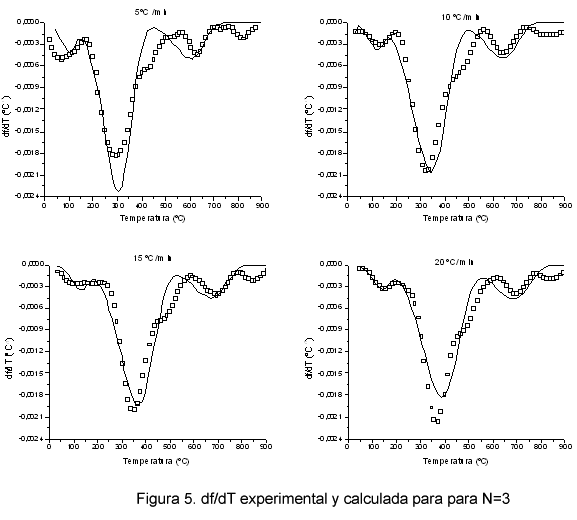
A continuación, suponiendo que la descomposición de los fangos ocurre mediante 3 fracciones independientes, se muestran en la Figura 4, las fracciones en peso experimental (puntos) y calculada (línea) y en la Figura 5 la derivadas de f respecto a la temperatura experimental (puntos) y calculada (línea).
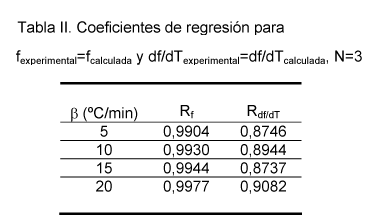
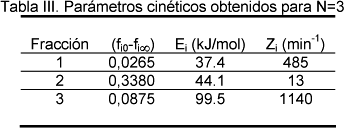
En la Tabla II se muestran los coeficientes de regresión lineal obtenidos suponiendo N=3 para las distintas β y en la Tabla III los parámetros calculados.
Como se puede observar la regresión es alta para todas las velocidades de calentamiento en todas las curvas de f, el coeficiente de regresión es menor para df/dT. En la Figura 5 se puede observar como las curvas experimental y calculada de df/dT muestran algunas diferencias, el pico mayor, que ocurre entre 200 y 550 ºC, muestra un hombro en el lado derecho, que no puede ser simulado con el modelo de 3 fracciones independientes. En la Figura 4 se observa como en el intervalo de temperatura en que se observa el hombro, la curva de f calculada se desvía de los puntos experimentales. Otra diferencia que se observa en la Figura 5 es el pico que aparece entre 800 y 900 ºC, y que puede corresponder a otra fracción que descompone a alta temperatura, probablemente debido a compuestos inorgánicos. Este pico, por ser el de menor magnitud, no se ha tenido en cuenta en el modelo, aunque podría incluirse otra fracción más.
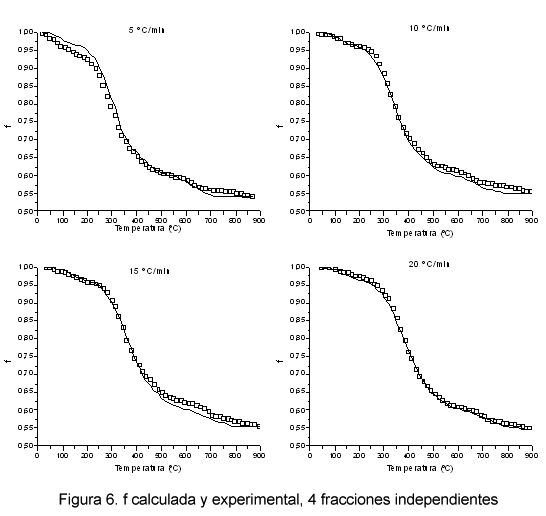
Con el fin de mejorar el ajuste de f, se ha considerado que la descomposición de los fangos en atmósfera inerte puede ocurrir mediante cuatro fracciones independientes. En la Figura 6 se muestran las curvas experimental y calculada de f para las cuatro β y en la Figura 7 las curvas de df/dT.
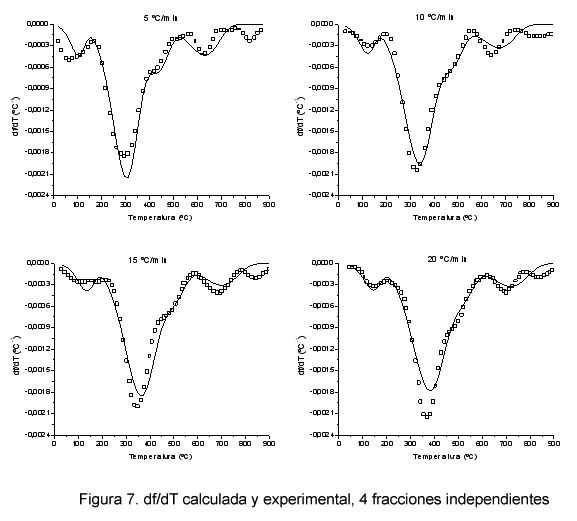
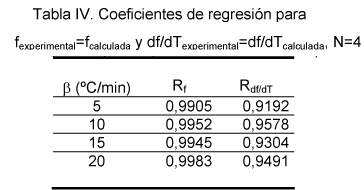
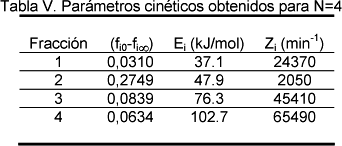
En la Tabla IV se muestran los coeficientes de regresión obtenidos para las curvas de f y df/dT y en la Tabla V los parámetros cinéticos.
4. Conclusiones
La pirólisis de fangos de depuradora a bajas velocidades de calentamiento (5 a 20 ºC/min) se puede describir satisfactoriamente teniendo en cuenta un modelo que supone la existencia de varias fracciones que descomponen independientemente. Con tres fracciones se alcanza un ajuste de las curvas experimentales de f, fracción en peso remanente durante la pirólisis, con coeficientes de regresión superiores a 0.99 para todas las curvas. Si se tienen en cuenta 4 fracciones el ajuste obtenido para las curvas de f es sólo ligeramente mejor que con 3 fracciones, sin embargo las curvas calculadas de df/dT sí que mejoran sensiblemente, ya que al incorporar una nueva fracción, el modelo se acerca más a las curvas halladas experimentalmente. Obviamente es necesario valorar, cuando se realizan modelos, si la complejidad del modelo justifica las mejoras que se obtienen en los ajustes, ya que con cuatro fracciones se usan 11 parámetros (4 energías de activación, 4 factores preexponenciales y 3 fracciones iniciales (fi0-fi"), mientras que con un modelo sencillo de orden n se usan únicamente tres (el orden n, la energía de activación y un factor preexponencial).
Agradecimientos
Los autores agradecen el soporte económico proporcionado por la Unión Europea dentro del programa ALFA-ALE Program (Thermochemical Conversion of Biomass, Project II - 0185 - FA). Los autores de Brasil agradecen a la FAPESP (Proc. # 98/15448-5 01/10841-5 y 01/08152-7).
Referencias
[1] J. WERTHER, T. OGADA; Sewage sludge combustion; Progress in Energy and Combustion Science; 25; pp. 55-116; 1999.
[2] D.T. FURNESS, L.A. HOGGETT, S.J. JUDD, Thermochemical treatment of sewage sludge, J.CIWEM, 14 (1), pp. 57-65, 2000.
[3] M. INGUANZO, A. DOMÍNGUEZ, J.A. MENÉNDEZ, C.G. BLANCO, J.J.PIS; On the pyrolysis of sewage sludge: the influence of pyrolysis conditions on solid, liquid and gas fractions; J. Anal. Appl. Pyrol.; 63 (1); pp. 209-222; 2002.
[4] J.A. CABALLERO, R. FONT, A. MARCILLA, J.A. CONESA; Kinetic model for the continuous pyrolysis of two types of polyethylene in a fluidized bed reactor; J. Anal. Appl. Pyrol.; 40-41; pp. 433-450; 1997.
[5] J.A. CONESA, A. MARCILLA, R. MORAL, J. MORENO-CASELES, A. PEREZ-ESPINOSA; Evolution of gases in the primary pyrolysis of different sewage sludges; Thermochim. Acta; 313 (1), pp. 63-73, 1998.
[6] D.L. URBAN, M.J. ANTAL, Study of the kinetics of sewage sludge pyrolysis using DSC and TGA; Fuel; 61 (9); pp. 799-806; 1982.
[7] X. CHEN AND S. JEYASEELAN; Study of sewage sludge pyrolysis mechanism and mathematical modeling; J. Environ. Eng.; 127 (7); pp. 585-593; 2001.
[8] P. HE, G. GU, L. SHAO AND Y. ZHANG; Research on low temperature thermo-chemical conversion to oil process for sewage sludge; Water Sci. Tech.; 42 (3-4); pp. 301-308; 2000.
[9] P. HE, L. SHAO, G. GU AND G. LI; Mechanism and kinetics of low-temperature thermochemical conversion process for sewage sludge; Water Sci. Tech.; 44 (10); pp. 341-347; 2001.
[10] F.L.P. RESENDE, A. GONZALO, J.L. SANCHEZ, J. ARAUZO; An integral model for the sewage sludge pyrolysis; 16th International Symposium on Analytical and Applied Pyrolysis "Pyrolysis 2004"; Alicante; Mayo 23-27; 2004a.
[11] F.L.P. RESENDE, A. GONZALO, J.L. SÁNCHEZ, L.A. TRUJILLO, L.M.G. ROJAS; Influence of experimental parameters on the pyrolysis of sewage sludge; 2nd World Conference and Technology Exhibition on Biomass, Roma, 10-14 Mayo 2004b.
[12] L.T. VLAEV, I.G. MASKOVSKA, AND L.A. LYUBCHEV; Non-isothermal kinetics of pyrolysis of rice husk; Thermochim. Acta; 406; pp.1-7; 2003.
[13] J.J.M. ÓRFÃO AND F.G. MARTINS; Kinetic analysis of thermogravimetric data obtained under linear temperature programming-a method based on calculations of the temperature integral by interpolation; Thermochim. Acta, 390 (1-2); pp.195-211; 2002.
[14] J.J.M. ÓRFÃO, F.J.A. ANTUNES, J.L. FIGUEIREDO; Pyrolysis kinetics of lignocellulosic materials - Three independent reactions model; Fuel (78); pp. 349-358; 1999.
[15] J.J. MANYA, E. VELO AND L. PUIGJANER; Kinetics of biomass pyrolysis: A reformulated three-parallel-reactions model; Ind. Eng. Chem. Res.; 42(2); pp. 434-441; 2003.
[16] J. A. CONESA, A. FULLANA, R. FONT; Thermal decomposition of meat and bone meal; J. Anal. Appl. Pyrol.; 70 (2); pp. 619-630; 2003.
[17] J.A. CONESA, A. MARCILLA, D. PRATS, M. RODRIGUEZ-PASTOR; Kinetic study of the pyrolysis of sewage sludge; Waste Management and Research; 15 (3); pp. 293-305, 1997.










 How to cite this paper
How to cite this paper