An. 5. Enc. Energ. Meio Rural 2004
Irradiação solar global em função da razão de insolação
Global solar irradiation in function of the insolation reason
Reinaldo Prandini RecieriI; Silvana QuallioII; Yuri FerruzziIII; Suedemio de Lima SilvaIV; Vitor Roberto Lourenço BatistaV
IProfessor do Curso de: Mestrado em Engenharia Agrícola e da Graduação em Biologia/UNIOESTE/FAG
IIAluna do Curso de Biologia/UNIOESTE
IIIAluno do Curso de Mestrado em Engenharia Agrícola/UNIOESTE. Professor FAG
IVProfessor do Curso de: Mestrado em Engenharia Agrícola e Graduação UNIOESTE/FAG
VAluno do Curso de Graduação em Engenharia Elétrica/FAG
RESUMO
O presente trabalho mostra a razão (Kt=RG/Ro) da irradiação solar global pela irradiação no topo da atmosfera na incidência horizontal em função da razão de insolação (n/N), objetivando-se encontrar uma equação para estimar a irradiação solar global diária na região de Cascavel/PR. Os dados experimentais foram obtidos na ESTAÇÃO AGROMETEOROLÓGICA do IAPAR (INSTITUTO AGRONÔMICO DO PARANÁ) montada na COODETEC/CASCAVEL-PR (Latitude 24,89ºS, Longitude 53,40ºO e altitude de 682m). A componente da irradiação solar global foi monitorada por um actinógrafo e a hora de brilho solar (n) através de um heliógrafo (R. FUESS BERLIN-STEGUTZ) num período de 17 anos, dos quais quatro foram utilizados na validação do modelo. A distribuição dos valores diários (Kt x n/N), relacionada através de regressão linear simples, forneceu uma equação de estimativa RG/Ro=0,16+0,40n/N com elevado coeficiente de determinação (R2 = 88,89%), na validação do modelo obteve-se um desvio variando de -9,76% a 11,44% com erro médio na ordem de 0,84%, estes valores estatísticos mostram que a irradiação solar global, na região de Cascavel, pode ser estimada com boa precisão.
Palavras-chave: irradiação global, índice de claridade, modelo de Angstron
ABSTRATCT
The present work shows the reason (Kt=RG/Ro) of global the solar irradiation for the irradiation in the top of the atmosphere in the horizontal incidence in function of the insolation reason (n/N), objectifying itself to find an equation esteem the daily global solar irradiation in the region of Cascavel/PR. The experimental data had been gotten in STATION AGROMETEOROLOGICAL of the IAPAR (AGRONOMIC INSTITUTE of the PARANÁ) mounted in the Coodetec/Cascavel-Pr (Latitude 24,89ºS, Longitude 53,40ºO and altitude of 682m). The component of global the solar irradiation was monitored by an actinograph and the hour of solar brightness (n) through a heliograph (R. FUESS Berlin-stegutz) in a period of 17 years, of which four had been used in the validation of the model. The distribution of the daily values (Kt x n/N), related through simple linear regression, supplied an equation of RG/Ro=0,16+0,40n/N estimate with raised determination coefficient (R2 = 88.89%), in the validation of the model got a -9,76% shunting line varying 11,44% with average error in the 0,84% order, these statistical values shows that global the solar irradiation, in the region of Rattlesnake, can be esteem with good precision.
INTRODUÇÃO:
As produções agrícolas, bem como o crescimento das plantas, são diretamente dependentes das variáveis climáticas, por exemplo da irradiação solar. Através do conhecimento dessas variáveis, as atividades agrícolas são definidas, sendo possível auxiliar o produtor agrícola, aumentando assim sua produtividade. A obtenção da medida da irradiação solar global é importante também para auxiliar em outras atividades tais como: engenharia, agronomia e zootecnia.
O alto custo dos instrumentos para medir as componentes da radiação solar, faz com que não seja observada de forma contínua na maioria das estações meteorológicas. Devido às dificuldades instrumentais, outra linha importante de estudo para a obtenção da irradiação global é a de modelagem. Nesta, as componentes da radiação solar são correlacionadas com diversos parâmetros meteorológicos, geográficos, atmosféricos e astronômicos, por exemplo, a temperatura, razão de insolação, latitude e outros que são mais facilmente medidos. Mediante a este fato, vários pesquisadores vem desenvolvendo modelos estatísticos e matemáticos para estimar a irradiação solar. Para que tenhamos boa precisão na estimativa da radiação solar, devemos ter uma série de dados confiáveis, o que leva alguns pesquisadores a criticar certos instrumentos de medidas, actinógrafo e heliógrafo. Comparando o trabalho de RICIERI et al. (1996), no qual determinou os parâmetros da equação de Angstron para a cidade de Botucatu/SP, utilizando uma série de dados obtidos através de um piranômetro EPPLEY-PSP conectado numa aquisição de dados da CAMPBELL SCIENTIFIC (instrumentos de precisão) e um heliógrafo para medir a hora de brilho solar, com o de TUBELIS (1988), que utilizou um actinógrafo e um heliógrafo para a mesma finalidade e mesmo local, constata-se que não houve diferença significativa entre os modelos apresentados.
Entre os pesquisadores, ANGSTRON (1924) foi o primeiro a propor um modelo estatístico para estimar a irradiação solar global, na horizontal, através da equação: RG/RC=α+(1-α)(n/N),onde:
RG = irradiação solar global;
RC = irradiação solar global em dias completamente limpos;
α= razão entre a irradiação em dia completamente nublado pela irradiação em um dia completamente limpo;
n= número de horas solar na superfície da Terra observadas em um dia;
N.= número máximo de horas de sol no topo da tamosfera em um dia.
Para obter os coeficientes desta equação é necessário possuir dados da irradiação solar global em dias completamente limpos, o que não é sempre possível. No intuito, de simplificar sua utilização, pesquisadores decidiram utilizar a irradiação no topo da atmosfera (Ro ), que é calculada com facilidade. PRESCOTT (1940) foi o primeiro pesquisador a modificar a equação de Angstron substituindo RC por Ro, determinada da seguinte forma: RG/Ro=a+bn/N.
Várias pesquisas realizadas mostram que as constantes a e b da equação de Angstron, variam de região para região. Entre os fatores que influenciam na variação destes parâmetros, estão a latitude, aerosol, umidade do ar, nebulosidade e a altitude local, GLOVER & MCCULLOCH (1958a). Fazendo uma análise destes parâmetros apresentados na literatura, RIETVELD (1978) concluiu que a se relaciona linearmente e b hiperbolicamente com valores médios da razão de insolação (n/N).
BLACK et al. (1954), GLOVER & MCCULLOCH (1958b) e MACKIENWICZ (1953) concluíram que os coeficientes variam em função da latitude, sendo que outros autores afirmam estar em função das características atmosféricas locais, podendo ser observada na determinação dos coeficientes da equação de Angstron, por diferentes partições. Este fato é observado com a comparação dos valores publicados, por exemplo, MOOLEY et al. (1962), STANHILL (1965) e YADAV (1965), encontrando diferença nos parâmetros obtidos com dados de médias mensais, diárias e semanais. A aplicabilidade das equações Kt=f(n/N) horárias estão direcionadas a áreas de interesses dos fenômenos instantâneos da radiação solar, tais como: meteorológico e aproveitamento da energia solar. Para aplicações agronômica e climatológica, onde a natureza dos fenômenos não são instantâneos, as partições das irradiações global e difusa são representadas em intervalos de tempo maiores, como diários ou mensais.
Propõe-se neste trabalho relacionar a razão da irradiação solar global na incidência horizontal pela irradiação no topo da atmosfera, com a razão de insolação (n/N), objetivando-se encontrar os coeficientes da equação de Angstron (RG/Ro=a+bn/N) para estimar a irradiação solar global na região de Cascavel/PR.
MATERIAL E MÉTODOS:
Os dados experimentais foram obtidos na ESTAÇÃO AGROMETEOROLÓGICA do IAPAR (INSTITUTO AGRONÔMICO DO PARANÁ) montada na COODETEC/CASCAVEL-PR (Latitude 24,89ºS, Longitude 53,40ºO e Altitude 682m), no período de janeiro de 1982 a dezembro de 1998.A radiação solar global (RGmed) foi monitorada, na horizontal, por um actinógrafo e a hora de brilho solar (n) através de um heliógrafo (R. FUESS BERLIN-STEGUTZ). Da série de dados, num total de 17 anos (1982 a1998), dos quais 13 anos (1982 a 1994) foram utilizados para determinar os coeficientes (a e b) da equação de Angstron, através de partição diária e 4 anos (1995 a 1998) para validar os valores da irradiação global (RGest) estimada pelo modelo. Os resultados foram analisados através do desvio Δ(%)=100(RGmed - RGest)/RGmed, do erro médio e frequência dos desvios.
Elaborou-se um programa em BASIC para calcular a hora do nascer e pôr do sol, declinação solar, irradiância solar no topo da atmosfera, cosseno do ângulo zenital (cosz) e a hora solar transformada em hora local. As equações de maior importância, utilizadas no programa, foram citadas por IQBAL (1983):

Sendo:
δ = declinação solar;
DJ = dia juliano;
ws = ângulo horário ao nascer do sol;
Φ = latitude local;
Γ = 2Π(DJ-1)/365,242;
Eo = fator de correção da excentricidade da órbita terrestre;
Et = Equação do tempo;
Ro = irradiância solar no topo da atmosfera (MJ/m2);
coszt = cosseno do ângulo zenital do Sol.
RESULTADOS E DISCUSSÃO:
A figura 1a, 1b são amostragem da série de dados, referente ao ano de 1994, mostram o comportamento da irradiação global e da razão de insolação, respectivamente. A irradiação global varia no intervalo de 1 a 23 MJ/m2, apresentando valores menores em torno do solstício de inverno, maiores no solstício de verão e intermediárias nos esquinócios de outono e primavera, enquanto que a variação da razão de insolação é melhor distribuída nas quatro estações do ano, no intervalo de 0 a 0,95 com média de 0,59.
A distribuição dos pontos experimentais diários (Kt x n/N) foi submetida em programa estatístico de regressão linear, obtendo-se o modelo empírico de Angstron (figura 2), RG/Ro=0,16+0,40n/N com coeficiente de determinação igual a 88,89%, mostrando boa precisão na estimativa da irradiação solar global local.
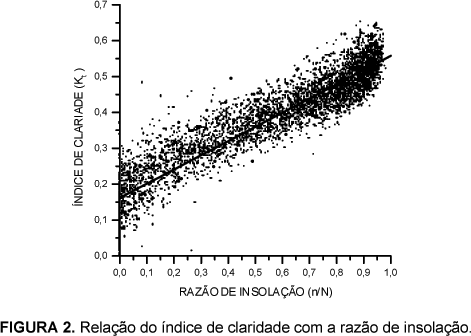
A analise dos limites da equação, mostra as características atmosféricas de Cascavel, quando n/N tende a zero, situação de elevada nebulosidade ou número de horas de brilho solar igual a zero, Ktmin é igual a 0,16, definindo o mínimo da radiação global que incide na superfície terrestre local. E quando n/N tende a 1, situação de ausência total de nuvens ou máximo de horas de brilho solar, Ktmax = 0,56 (Kt = a + b) definindo a transmissividade máxima da radiação global.
O valor máximo de Kt encontrado nos dados experimentais foi de 0,701 e mínimo de 0,002, comparados com Ktmax e Ktmin, pode-se observar que a equação de Angstron tende a superestimar a irradiação global em dias completamente nublados e subestimar em dias de céu totalmente limpo.
A curva de freqüência dos desvios apresentados na figura 3, mostra uma tendência de distribuição em torno de 0% com, 279 dias entre 0 e 5%, 259 dias entre 0 e -5%, 172 dias 5 e 10%, 165 dias entre -5 e -10%, 102 dias 10 e 15%, 92 dias entre -10 e -15%, 59 dias entre 15 e 20%, 52 dias entre -15 e -20%, 43 dias entre 20 e 25%, 20 dias entre -20 e -25%, 21 dias entre 25 e 30%, 14 dias entre -25 e -30%, totalizando 676 dias no intervalo positivo e 602 dias no intervalo negativo. Estes valores mostram que o modelo tem uma tendência de superestimar a irradiação.
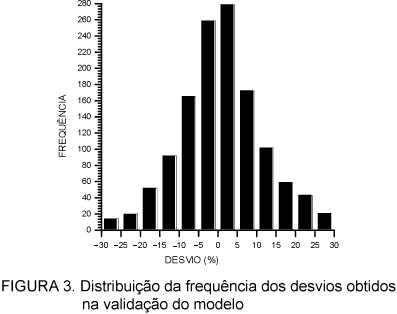
Através do cálculo da média dos desvios diários, obteve-se um desvio variando de -9,76% a 11,44% com erro médio na ordem de 0,84%, o qual mostra que, no geral, os valores da irradiação estimadas pelo modelo são superestimados, confirmando o que foi discutido anteriormente.
CONCLUSÕES:
Estatisticamente a irradiação solar global, na região de Cascavel, pode ser estimada com boa precisão.
A equação de Angstron tende a superestimar a irradiação global em dias completamente nublados e subestimar em dias de céu totalmente limpo.
No geral, o valor da irradiação solar estimada, através do modelo de Angstron é, superestimado.
AGRADECIMENTOS:
Instituto Agronômico do Paraná (IAPAR/Londrina) - Área de Ecofisiologia.
REFERÊNCIAS BIBLIOGRÁFICAS
ANGSTRON, A. 1924. Solar and terrestrial radiation.Q.J. R.Meteorol.Soc., 50: 121-25.
BLACK, J.N., BONYTHON, C.W., PRESCOTT, J.A., 1954. Solar radiation and the duration of sunshine. Q.J.R. Meteorol. Soc., 80: p.231-235.
GLOVER, J., MCCULLOCH, J.S.G., 1958a. The empirical relation between solar radiation and hours of sunshine in high-altitude tropics. Q.J.R. Meteorol. Soc., 84 : p.56-60.
GLOVER, J., MCCULLOCH, J.S.F., 1958b. The empirical relation between solar radiation and hours of sunshine. Q.J.R. Meteorol. Sco., 84: 172-175.
IQBAL, M. An introduction to solar radiation. Academic Press, New York, 390p. 1983.
MCKIENWICZ, M. The space distribution of insolation in Poland. Acta Geophys. Pol., 1: p.100-25, 1953.
MOOLEY, D.A., BEDEKAR, V.C., RAGHAVAN, S., 1962. Relation between solar radiation and the duration of bright sunshine at Madras. Indian J. Meteorol. Geophys., 13: p.510-515.
PRÈSCOTT, J.A. Evaporation from a water surface in relation to solar radiation. Transactions of the Royal Society of South Autralia. v.64, p.114-118, 1940.
RICIERI, R.P., ESCOBEDO, J.F., MARTINS, D. Relações da radiações solar difusa e global em Botucatu. In: CONGRESSO BRASILEIRO DE METEOROLOGIA, IX, 1996, Campos do Jordão. Rio de Janeiro: Sociedade Brasileira de meteorologia, 1996. p.547-550.
STANHILL, G., 1965. A comparison of four methods of estimating solar radiation. UNESCO Arid Zone Res., 25: 55-61.
TUBELIS, A. Metodologia descritiva: Fundamentos e aplicações brasileiras. Nobel, São Paulo-SP. 374p., 1988.
YADAV, B.R., 1965. Total solar radiation in relation to duration of sunshine. Indian J. Meteorol. Geophys., 16: 261-266.










 How to cite this paper
How to cite this paper