An. 5. Enc. Energ. Meio Rural 2004
Mathematical modelling of wood and briquettes torrefaction
Felix Fonseca FelfliI, *; Carlos Alberto LuengoI; Pedro Beaton SolerII; José Dilcio RochaIII
IFGW/DFA/GCA, Universidade Estadual de Campinas, CP 6165, 13083-970, Campinas, SP, Brasil
IICentro de Estudios de Eficiencia Energética, Facultad de Ingeniería Mecánica, Universidad de Oriente, Santiago de Cuba, Cuba.
IIINúcleo Interdisciplinar de Planejamento Energético - NIPE/UNICAMP e Bioware Tecnologia, www.bioware.com.br, Campinas-SP, Brasil
ABSTRACT
A mathematical model valid for the torrefaction of wood logs and biomass briquettes is presented. The model described both chemical and physical processes, which take place in a moist piece of wood heated at temperatures between 503 and 573K. Calibration measurements of the temperature profile and mass loss, were performed on dry cyllinders of wood samples during torrefaction in an inert atmosphere at 503, 533, and 553K. The calculated data shows a good agreement with experiments. The model can be a useful tool to estimate projecting and operating parameters for torrefaction furnaces such as minimum time of torrefaction, energy consumption and the mass yield.
Keywords: Modelling, Torrefaction, Biomass.
RESUMO
Neste trabalho é apresentado um modelo matemático que descreve o processo de torrefação de madeira e briquetes de biomassa. O modelo descreve os fenômenos físicos e químicos que ocorrem durante a torrefação de uma peça úmida de madeira aquecida entre 503 e 573K. Durante o estudo foram determinados os perfis de temperatura e a variação de massa de um cilindro de madeira submetido a temperaturas de 503, 533 e 553K em uma atmosfera inerte. Os resultados da simulação mostraram adequado ajuste com os resultados experimentais obtidos. Este modelo matemático pode ser uma ferramenta para estimar parâmetros de projeto e operacionais, tais como tempo mínimo de torrefação, consumo energético do processo e rendimento do processo.
1. Introduction
Torrefaction is a feasible method for improvement of the properties of biomass fuels. Biomass torrefaction takes place at low heating rate and temperatures between 503 K and 573 K in inert atmosphere. Torrefied biomass has advantageous properties such as low moisture, lower smoke emission and an increased heating values. Torrefied biomass can be used in several applications such as fuel for domestic cooking stoves, barbecue, residential heating, and for industrial applications [1].
In order to desing a torrefaction furnace [2] it is necessary to know parameters such as minimum time of torrefaction, energy consumption and the mass yield [3]. This work introduces a mathematical model, which allows estimating these parameters. It also describes both chemical and physical processes, which take place in a wet piece of biomass during torrefaction. Since this process takes place at relatively low temperatures, chemical reactions are not frequent, simplifying the modeling. It is important to emphasize that modelling of small biomass particles pyrolysis process is widely studied, including highly complex models [4-6]. However, the relatively simpler model proposed here is intended for estimating useful parameters of the torrefactor during the torrefaction of briquettes or wood logs.
2. Model description
When a briquette or a wood log is subjected to temperatures ranging from 503 K to 573 K, heat is conducted inwards the solid producing both a drying and a pyrolysis front, which propagate with a velocity proportional to heat flux. The drying front moves ahead of the pyrolysis front. The bound and free water move outwards the solid by diffusion and capillarity, and the water vapor move outwards by convection and diffusion mechanisms. A small portion of water vapor is recondenses inward the unreacted solid.
The pyrolysis reactions take place at the surface when the temperature approaches 453 K, forming a pyrolysis zone which moves inwards as the unreacted layer of the solid heats up. This effect creates a front of primary degradation reactions with an endothermic nature. The exothermic reactions start at 523 K, but these are negligible in comparison to endothermic reactions below 573 K. During the torrefaction process, no secondary reactions occur, so there is not enough production of secondary char and gas because the temperatures are not high enough. The volatiles move outwards by convection mechanism, creating the cooling effect due to the heat exchange in the external layers where the temperature is higher. As the reactions proceed, the physical and chemical properties of solid vary causing changes in solid heating rates. Geometrical changes may occur such as shrinking and fissuring.
To model the aforementioned process assumptions based on previous studies [7,8] are proposed: (i) heat and mass transfer phenomena are one-dimensional; (ii) no geometrical changes occur throughout torrefaction; (iii) volatile and water vapor are in thermal equilibrium with the solid; (iv) diffusive transport of species within the pores is negligible; (v) Bound-water movement is negligible; (vi) no recondensation of water vapor occurs; (vii) the solid permeability is high enough for the pressure gradients to be negligible; (viii) the energy stored in the gas phase is negligible.
The torrefaction kinetics is based on a three-reaction scheme in which competing primary two-step reaction pyrolyze biomass to gas (K1), tar (K2) and charcoal (K3). The primary pyrolysis reaction rates are represented with an Arrhenius-type temperature dependence and first-order with respect to the mass of unreacted biomass [8-14]. In this type of reaction scheme, solid conversion and volatile emissions can be studied separately.
Several drying models are proposed [7,8,11-14], they all assume that a drying front exists and moves inwards the inner layers. In this work, the scheme proposed by Chan Wai-Chun R. et al. [8] is used, where the drying process is considered as an additional chemical reaction that occurs simultaneously with pyrolysis. The evaporation rate is represented by the Arrhenius expression,

Where rev is the moisture evaporation rate (kgm-3s-1), x is the moisture fraction in the solid, ρw is the biomass density (kgm-3), Ao a pre-exponential factor (s-1), Eo is the activation energy (kJmol-1), R represents the gas constant (kJmol-1K-1) and T is the temperature (K). This expression is implemented numerically together with the pyrolysis rate also expressed by an Arrhenius type expression.
3. Mathematical formulation
The model solves for the conservation equations of species and energy in a solid matrix. To solve the resulting set of differential and algebraic equations, the method of finite-differences for parabolic differential equations was applied.
The solid species conservation equations are written:

Where ρw and ρc are respectively the apparent density of wood and charcoal (kgm-3), and K1, K2, and K3 are the species reaction rates according the kinetic scheme (see equation 10).
Gaseous species balance equation is:

Where ρg is the volatile (gas and tar) mass concentration (kgm-3), u is the volatile velocity (ms-1) and n represents a geometric parameter (n = 1 for cylinder shape and n = 0 for slab shape).
The moisture balance equation is:

Where χ is the moisture fraction in the wood, and rer is the moisture evaporation rate (equation 1).
The water vapor continuity equation is:

Where ρv is the water vapor density (kgm-1) and u is the water vapor velocity (assumed equal to volatiles velocity)
The energy conservation equation is:
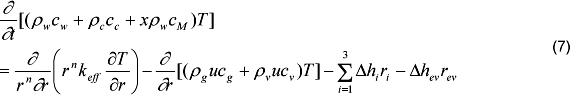
Where cw, cc, and cM are the specific heats (kJkg-1K-1) of the wood, char and moisture, T is the temperature (K) in the solid matrix, keff (kWm-1K-1) is the effective heat conductivity (equation 8), δhi is the heat of chemical reaction (kJ/kg), ri is the conversion rate species (equation 11) and δhev is the heat for moisture evaporation (kJkg-1).
The effective conductivity is calculated from:

Where kw and kc are the heat conductivities of the wood and char, the interpolation factor Φ is calculated from:

Reaction rates are calculated from:

Conversion rates species are calculated from:
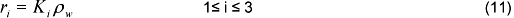
The initial and boundary conditions are written:
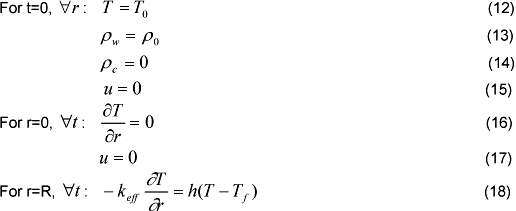
Where To is the room temperature, Tf is the torrefaction temperature, h is the convection heat transfer coefficient and ρo is the initial density of the substrate. The heat transfer in the boundary layer is assumed by convection only, and the heat flux is incident at fixed temperature.
Instantaneous rate of heat transfer in the solid is calculated from:

Where r is the wood log (briquette) radius, l is the wood log length.
The heat consumption rate in the process is calculated from:

In all equations t is the time and r is the radius or linear dimension in the direction of heat and mass transfer.
4. Validation of the model
The validation of the mathematical model was obtained using a dry sample. It was used an electric furnace equipped with a temperature control system, a nitrogen flow of 5 liters per hour was used to ensure an inert atmosphere. A couple of thermocouples were positioned inside and out the furnace for authomatic temperature control and third one monitored the center of the sample.
The calibration samples were Pinus cyllinders (20 mm in diameter and 40 mm in length). The thermocouple in the center of the sample was 1 mm in diameter. Measurement error bars were ±1K. During experiments, the temperature of each sample was measured as a function of time. When the temperature at the center reached the external temperature the experiment was stopped and the average mass loss determined. The above experimental procedure was carried out in the electrical furnace at temperatures of 403, 503, 533 and 553 K, and repeated to verify reproducibility.
Kinetic data used in the validation was obtained in the literature on the topic [8,12,13] (where A1=1.3×108 s-1, A2=2×108 s-1, A3=1.08×107 s-1, E1=140 kJmol-1, E2=133 kJmol-1, E3=121 kJmol-1, Δh1= Δh2= Δh3=418 kJkg-1) as well as the physical properties (ρo=370 kgm-3, cw=1.5 kJkg-1K-1, cg=cc=1.1 kJkg-1K-1, kw=16×10-2 Wm-1K-1, kc=7.1×10-2 Wm-1K-1).
The heat transfer coefficient inside the furnace was estimated applying equations for an inert cylinder submitted to a convective heat flow under transient conditions. A wood sample was inserted in the furnace at a temperature of 403 K, the temperature profile being defined according to the time. Based on this data, the average heat transfer coefficient was estimated according to Biot & Fourier criteria, and the average value defined for these conditions was 16 Wm-2K-1.
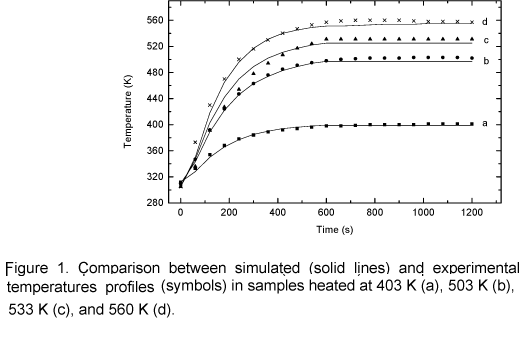
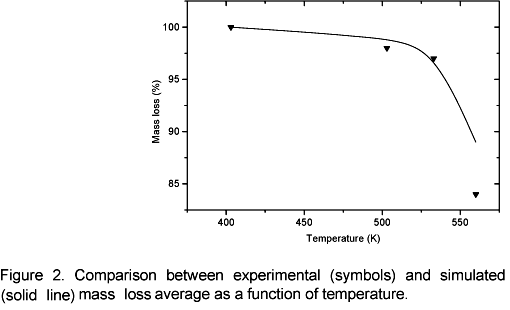
Figure 1 shows a close correlation between the experimental and theoretical temperature profiles. It can be noticed that when temperature reaches 403 K, the data correlation is closer than on other conditions. This probably happens because the model was not simplified in this phase process, since no chemical reactions take place at this temperature although the sample is heated. For temperatures above 503 K, simulated values are lower than experimental data at the end of the curve. This probably occurs due to weak, parasite carbonization reactions they have not been considered. Those reactions have an exothermic nature; therefore the sample temperature is higher than the external temperature at the end of the heating process. The average mass loss as a function of temperature is shown in figure 2. The agreement between the model and experimental data is good in the temperature range 503 K to 533 K, however for 553 K the model lags experimental data. It is suspected that this occurs because carbonization reactions (cellulose and lignin degradation) start to be important as the temperature approaches to 553 K, so exothermic reactions start increasing the heating rate in the solid matrix and consequently the mass loss is increasing too. This effect is not included in the model. It is important to emphasize that during torrefaction the major decomposition reactions concern hemicellulose.
6. Modelling results
The torrefaction was simulated for a cylindrical wood log in order to examine the main parameters of the process, such as drying, torrefaction time, energy consumption and mass loss average. The wood log dimensions were those currently considered for the carbonization process in Brazil, that is, 0.1 m in diameter and 0.5 m in length. The assumed moisture was 15% and the heat transfer coefficient inside the furnace assumed was 60 Wm-2K-1. Kinetic data considered to simulate the drying process was A0= 5.13 106 s-1, Eo = 88 kJmol-1, δhev= 2257 kJkg-1 [8]. The simulation was performed for eucalyptus wood with a density of 500 kgm-3. The heating gas temperature for torrefaction was 573 K.
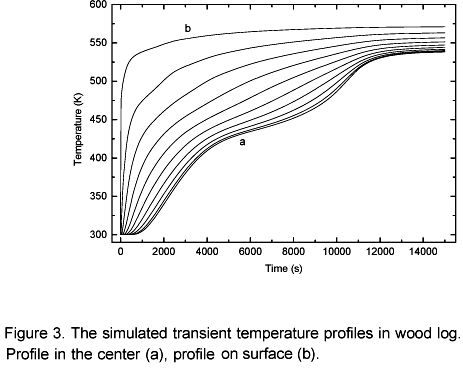
Figure 3 shows temperature profiles in 10 different points in the log; the distance between the points is 0.005 m, which is the spatial distribution of the numerical analysis. As shown, the log surface is rapidly heated, making the surface physical chemical properties vary in a fast and distinguished manner with regard to others regions in the log. Thus, the conduction heat transfer to the interior of the log becomes harder as the successive layers of the wood are torrefied. Based on this, it is concluded that there is a log optimum residence time. Figure 3 shows that after 3.3 hours the homogeneousness of the temperature inside the log becomes more and more difficult. In the layers next to the center of the log the heating process is interrupted at a temperature range of 393 K to 423 K (drying plateau). At this temperature range the drying occurs, the biomass pyrolysis starts, the local energy consumption is higher so the temperature rises is delayed. In the layers next to the surface no drying plateau is observed, this occurs due to a heat flux transfer in those layers is much more intense than the local heat needed for the moisture evaporation so, the evaporation occurs instantaneously.
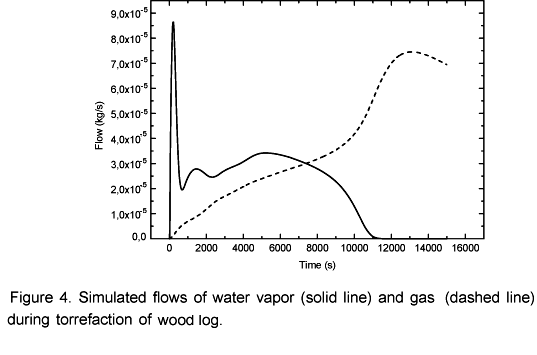
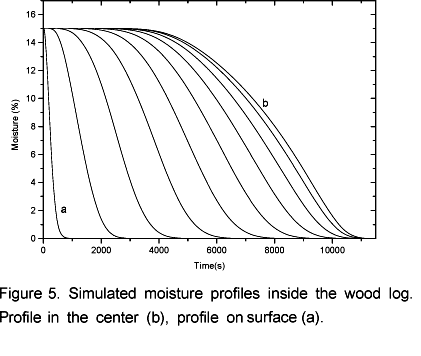
The simulations of volatile and water vapor emissions are shown in Figure 4. At the beginning of the process an intense emission of water vapor takes place and then the emission level decreases. This occurs because there is a strong heating in the layers next to the surface (Figure 3) resulting in an intense drying. This way, when the moisture in those layers is evaporated the vapor flow becomes relatively low because the inner layers have not yet reached the temperature observed at the beginning of the drying process. Simultaneously to the drying process the pyrolysis takes place in the superficial layers. That is why in the beginning of the process it can be observed a constant increase in the volatile emissions. After 0.5 hours the vapor flow becomes more intense again until it reaches another peak when it begins to decrease to zero after 3 hours and 10 minutes. At this point biomass is completely dry as shown in Figure 5. Simultaneously, the volatile flow is kept constant up to 3.6 hours and then it starts to decrease. Afterwards, the temperature inside the log exhibits an asymptotic behavior.
Based on the previous simulation, it is possible to estimate some useful parameters for the torrefaction furnaces desing. For example, under simulated conditions the total torrefaction time should be 4 hours and 10 minutes, the average heating rate of 0.09 kWkg-1 (calculated by equations 20 and 21) with 72 % of mass yield and consequently a volatiles emission of 0.13 kgh-1 and water vapor of 0.1 kgh-1. This data applies to a whole set of logs under torrefaction conditions.
6. Conclusions
Calculated values using the model presented a good agreement with experimental data, validating the assumptions and simplifications used. During the simulation it was observed an optimum residence time for wood logs with a relatively large diameter (above 5 cm). As the torrefaction zone propagates into the solid, the char thicknesses increased. As consequence the unreacted core is insulating (the heat conductivity decreases) and the rise in the temperatures tend to flatten, making it difficult to homogenize the temperature profiles inside the log. The mathematical modelling can be used as a tool to estimate parameters for desining and operating torrefaction systems such as minimum torrefaction time, drying and torrefaction rates, flows of volatiles and water vapor and energy consumption in a set of briquettes or wood logs.
Acknowledgments
The authors acknowledge the financial support of FAPESP 99/01064-3, 02/03215-3, 01/08152-7, 01/10841-5, and 03/13313-5, F.F.F. thanks G. Capobianco and S. Franco for helping the experiments also C.A.L acknowledges M. J. Antal for the early motivation of this research.
References
[1] Bourgeois, J P., Guyonnet, R. 1985. Torrefied wood from temperate and tropical species, advantages and prospects. In: Egneus and Ellegard, editors. Bioenergy 84, Volume III. London 1984. p. 153-159.
[2] Fonseca Felfli F., Luengo C. A. and Beaton P. A. A Furnace for wood and lignocelluloces briquettes torrefaction, and method for producing torrefied lignocelluloces material. BR Pat., n. PI0300090-7.
[3] Fonseca, F. F., Luengo, C. A., Beaton, P. A. A numerical model for biomass torrefaction.. In: H. Kopetz, Weber, Palz, Chartier and Ferrero, editors. Biomass for Energy and Industry. Wurzburg; 1998. p. 1596-99.
[4] Kothari V. And Antal, M.J. Numerical studies of the flash pyrolysis of cellulose. Fuel 1985; 64:1487-93.
[5] Antal M. J. Mathematical modelling of biomass pyrolysis phenomena. Fuel 1985; 64:1483-86.
[6] Di Blasi C. A Transient, two-dimensional model of biomass pyrolysis. In: Bridgwater A V, and Boocock DGB, editors. Developments in thermochemical biomass conversion. London: Blackie Academic and Professional; 1997. p. 489-529.
[7] Alves S.S. and Figueiredo J.L. A model for pyrolysis of wet wood. Chemical Engineering Science 1989; 44:2861-9.
[8] Wai-Chun R. Chan, Kelbon M. And Kriger B. Modelling and experimental verification of physical and chemical processes during pyrolysis of a large particle. Fuel 1985;64:1505-14.
[9] Di Blasi C. And Russo G. Modelling of transport phenomena and kinetics of biomass pyrolysis. In: Bridgwater A V, and Boocock DGB, editors. Developments in thermochemical biomass conversion. London: Blackie Academic and Professional; 1994. p. 906-22.
[10] Larfeld J., Leckneer B. and Malaaen MC. Modelling and measurements of the pyrolysis of large wood particles. Fuel 2000;79:1637-43.
[11] Malaaem M.C, Grønli MG. Modelling and simulation of moist wood drying and pyrolysis. In: Bridgwater A V, and Boocock DGB, editors. Developments in thermochemical biomass conversion. London: Blackie Academic and Professional; 1994.p. 132-46.
[12] Kenneth M. B, Kenneth W. R., Christopher J. R. Modeling thermally thick pyrolysis of wood. Biomass and Bioenergy 2002; 22: 41-53.
[13] Kenneth M. B, Mathew J. H. Modeling the combined impact of moisture and char shrinkage on the pyrolysis of a biomass particle. Fuel 2003; 82: 1633-44.
[14] Bilbao R., Mastral J. F., Ceamanos J., And Aldea M. A. Modelling of the pyrolysis of wet wood. Journal of Analytical and Applied Pyrolysis 1996; 36: 81-97.
* Present Address: BIOWARE - Centro de Tecnologia da UNICAMP, Rua Bernardo Sayon, No. 100, sala 207, 13083-866, Barão Geraldo, Campinas-SP. Tel: (19) 3788-4996 E-mail: fffelfli@hotmail.com










 How to cite this paper
How to cite this paper