An. 5. Enc. Energ. Meio Rural 2004
Modelo para a simulação de uma microturbina
Felipe Samuel de Bona; Ernesto Ruppert Filho
IEstudante de Mestrado da Faculdade de Engenharia Elétrica e de Computação da Unicamp (FEEC/UNICAMP)
IIProfessor e Pesquisador da Faculdade de Engenharia Elétrica e de Computação da Unicamp (FEEC/UNICAMP)
RESUMO
A geração distribuída (GD) está entrando no mercado mundial de eletricidade rodeada de promessas e incertezas. Sendo assim, ferramentas de simulação são necessárias para melhor se avaliar os possíveis benefícios e as possíveis complicações decorrentes da utilização da geração distribuída no sistema elétrico. Esse artigo visa apresentar um modelo para a simulação de um dos mais promissores tipos de geração utilizados na GD, que é a geração de energia elétrica através de microturbinas.
Palavras chave: Microturbina, modelo, geração distribuída.
ABSTRACT
The introduction of distributed generation (DG) units in the electric power system has been surrounded by many promises and uncertainnesses. Hence, new simulation tools are needed in orther to assess the issues and the benefits related to the connection of DG in the electric power system. In this paper will be presented and simulated a model of a microturbine, a new and emerging distributed generation technology.
Introdução
Uma das tecnologias mais utilizadas com geração distribuída é a das microturbinas. As microturbinas são conversores eletromecânicos de energia que convertem a energia mecânica proveniente da combustão do gás natural (ou diesel, propano, biogás) em energia elétrica.
Devido ao processo de obtenção da energia mecânica, a velocidade angular adquirida pelo eixo é da ordem de 50000 à 10000 rpm. Qualquer que seja o gerador elétrico a ser acoplado ao eixo da turbina ele deverá gerar energia elétrica com tensão alternada senoidal em freqüência correspondente à rotação do eixo que obviamente será elevada.
No caso de um gerador síncrono de 2 pólos movido a uma rotação de 60000 rpm a freqüência da tensão alternada obtida em seus terminais será de 1000 Hz. Essa freqüência é muito maior do que as freqüências usuais de 50 e 60 Hz dos sistemas de energia elétrica e portanto, inaceitável. Outro problema que ocorre é relativo à amplitude dessa tensão que precisará ser controlada para se ter valores padronizados pelos diferentes sistemas elétricos existentes no mundo.
A compatibilidade da freqüência e da amplitude da tensão nos terminais do gerador é feita por conversores eletrônicos de potência ligados aos terminais do gerador. O objetivo deste trabalho é apresentar um modelamento completo do sistema denominado microturbina baseado na literatura existente (Lasseter, 2001) e com ele realizar, usando o software Simulink® (SimPowerSystem Toolbox), uma simulação do seu desempenho dinâmico incluindo os controladores necessários.
O sistema da microturbina
A figura 1 mostra esquematicamente o sistema em estudo. Trata-se da microturbina de um único eixo que é a mais utilizada comercialmente e que atinge a velocidade de 50000 a 10000 rpm no gerador elétrico.
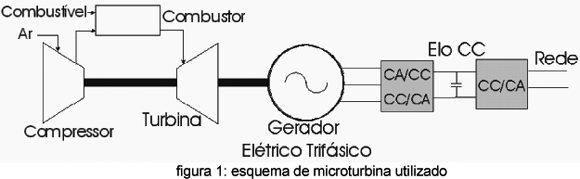
No combustor o ar comprimido proveniente do compressor mistura-se com o combustível. A mistura alimenta um processo de combustão contínua, responsável por gerar a energia térmica que será transformada em energia mecânica nas pás da turbina. O compressor é movido através do consumo de parte dessa energia mecânica, a outra parte da energia mecânica é transformada em energia elétrica pelo gerador elétrico. Como se pode visualizar na figura 1, o compressor, a turbina e o gerador elétrico estão conectados ao mesmo eixo girante.
O gerador elétrico, em geral síncrono de imã permanente, produz em seus terminais tensão alternada de amplitude e de freqüência indesejadas que são compatibilizadas pelos conversores eletrônicos de potência. O primeiro conversor é um retificador trifásico (conversor CA/CC) que pode ser controlado ou não controlado e que transforma a tensão alternada de alta freqüência em tensão continua. O segundo conversor é um inversor trifásico (conversor CC/CA) que transforma a tensão contínua em tensão alternada de freqüência 50 ou 60 Hz. A amplitude da tensão pode ser controlada pelo retificador e pelo inversor ou só apenas pelo inversor.
Entre o retificador e o inversor há um elo de corrente contínua constituído de um ultracapacitor ou de uma bateria que se responsabiliza pelo armazenamento de energia que é usada quando ocorrem bruscas variações de carga. O armazenamento de energia é necessário porque a microturbina não possui inércia suficiente para armazenar energia cinética para essas situações dinâmicas.
Existe uma outra configuração para a microturbina que utiliza uma engrenagem para diminuir a velocidade que o rotor do gerador elétrico é submetido. Esse gerador elétrico, normalmente um gerador síncrono ou de indução produz diretamente tensão de amplitude e de freqüência compatíveis com a da rede, livrando assim a microturbina da necessidade de utilizar conversores eletrônicos de potência. Em contrapartida, essa configuração exige um controle de velocidade para a microturbina e um controle de excitação do gerador elétrico. Um modelo para dessa configuração de microturbina é apresentado na referência (Tomsovic, 2002).
Gerador elétrico
Geradores síncronos de imã permanente são utilizados como meio de se gerar eletricidade em sistemas de geração eletromecânica que trabalham com velocidades variáveis como geradores eólicos, microturbinas e volantes (Cengelci, 2000).
De modo geral um gerador síncrono de imã permanente têm as mesmas características de um gerador síncrono convencional, a maior diferença é a utilização de imãs permanentes no rotor para se gerar o campo ao invés de um enrolamento energizado. As principais vantagens da utilização desse gerador são: a) ausência de escovas no gerador, o que diminui a necessidade de manutenção no gerador da microturbina; b) o diâmetro do rotor pode ser bem pequeno, diminuindo assim o valor da força centrífuga que nele atua; c) o gerador apresenta menor peso e dimensões; d) ausência de perdas ocasionadas por correntes no rotor.
O circuito equivalente de um gerador de imã permanente (GIP) em coordenadas dqo é apresentado na figura 2 (Mung, 1997). Lmd e Lmq são as indutâncias de magnetização equivalentes no eixo d e q. Lls é a indutância de dispersão e Rs é a resistência dos enrolamentos do estator. A corrente i´m é a corrente de magnetização equivalente dos imãs permanentes referida ao estator.
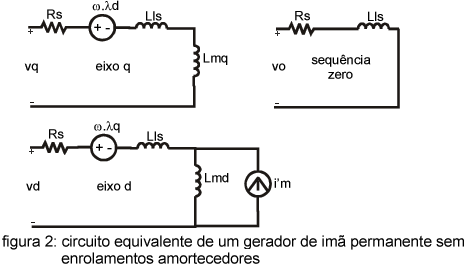
O gerador elétrico da microturbina não é submetido a bruscas variações de carga durante sua operação pois estas são absorvidas primeiramente pelas baterias. Sendo assim, ao contrário dos geradores elétricos diretamente conectados à rede, o gerador elétrico utilizado na microturbina não apresenta enrolamentos amortecedores. As equações de tensões (em coordenadas dqo) do GIP são apresentadas nas equações (1) à (3) onde λ representa o fluxo concatenado em cada um dos eixos d, q e o. A equação (4) determina o torque eletromagnético do gerador (Tem), onde P é o número de pólos do gerador.
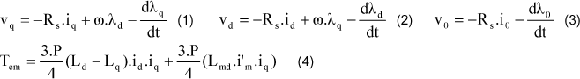
onde:
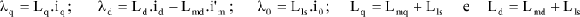
Conversor CA/CC
Por motivo de simplicidade utilizou-se no modelo um retificador trifásico não controlado de onda completa. Este modelo já está pronto na biblioteca do toobox SimPowerSystem, do programa Simulink®. O esquema do retificador e a forma de onda da tensão (VL) gerada pelo mesmo podem ser visualizados na figura 3. O ripple presente na forma de onda da tensão VL, que é característico dos retificadores, é quase que inteiramente suprimido pela bateria e pelo capacitor que são conectados à saída do retificador (no elo CC).
Elo de Corrente contínua
Como já dito anteriormente a microturbina necessita de algum tipo de reserva de energia para conseguir suportar grandes variações de cargas. O local mais apropriado para se conectar esse armazenamento de energia é o elo CC.
As baterias de chumbo-ácido são tipicamente utilizadas em veículos elétricos, no-breaks, e como fontes de energia para partidas de motores de combustão interna. Elas são de baixo custo, apresentam um baixo auto-descarregamento e tem a capacidade de prover altas correntes durante um curto espaço de tempo. Essas características tornam as baterias de chumbo-ácido as mais apropriadas para utilização em microturbinas (Illindala, 2002).
Um modelo simplificado de uma bateria, utilizado na simulação, é apresentado na figura 4a (Illindala, 2002). O capacitor C representa a capacidade de carga da bateria, o resistor em paralelo com o capacitor (Rad) representa o auto-descarregamento da bateria e tem um valor muito alto para o caso de baterias de ácido-chumbo. Por último, a resistência Ri representa a resistência interna da bateria.
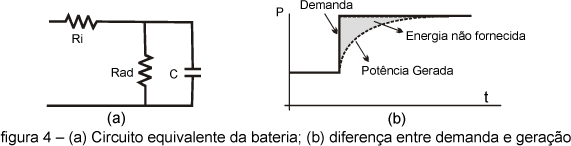
Quando há uma variação de carga nos terminais da turbina, cria-se uma diferença entre a nova demanda e a potência gerada pela mesma (veja figura 4b). Essa diferença acarreta numa diminuição da tensão no elo CC e, portanto, no nível de tensão que pode ser gerado pelo inversor. A capacidade da bateria deve ser cuidadosamente ajustada para contrabalancear essa diferença de energia de modo que os limites de tensão de operação das cargas não sejam ultrapassados.
É importante ressaltar que as baterias especificadas devem ter tanto um rápido descarregamento como um rápido carregamento, de modo a conseguir liberar e absorver a energia rapidamente a energia do elo CC quando necessário.
A fim de eliminar de uma maneira mais eficiente a tensão de ripple no elo CC, foi colocado no modelo da microturbina um capacitor em paralelo com o modelo da bateria. Apesar deste capacitor ter uma capacidade de armazenamento pequena, ele é mais eficiente que a bateria para suprimir o ripple pelo fato de não ter uma resistência interna.
Conversor CC/CA
O conversor CA/CC é responsável pela geração da forma de onda da tensão de saída da microturbina. Na maior parte das microturbinas, se utilizam inversores controlados por modulação em largura de pulso (MLP ou PWM). As chaves semicondutoras utilizadas são IGBT (Insulated Gate Bipolar Transistor - transistor bipolar de porta isolada). A técnica específica de modulação de cada fabricante não é revelada na literatura. Na simulação deste artigo utiliza-se uma modulação através da técnica de vetores espaciais em duas dimensões.
Com o objetivo de tornar a simulação mais rápida e simples, o inversor foi construído com modelos de chaves ideais, controladas pelos 6 sinais que partem do controle do inversor.
Os possíveis estados de comutação (V1, V2... V8) que o inversor pode apresentar, dado que a fonte de tensão de corrente contínua não pode ser curto-circuitada e que a corrente de saída do inversor não deve ser interrompida, são restritos aos apresentados na figura 5. Na tabela da figura "0" indica que a chave esta aberta e "1" que está fechada. As chaves de uma mesma perna são complementares (quando uma fecha a outra abre).
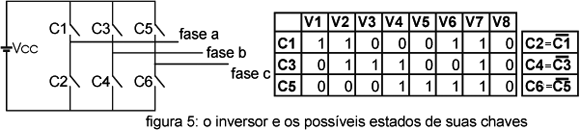
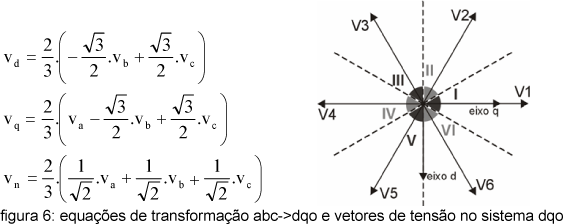
Essas configurações resultam em diferentes tensões na saída do inversor, que podem ser representadas por vetores no sistema d-q-n. As equações de transformação das tensões a-b-c para d-q-n, bem como os vetores produzidos pelos diferentes estados das chaves são apresentados na figura 6. O modelo de inversor apresentado alimenta somente cargas balanceadas, deste modo a equação de vn apresentada na figura 6 torna-se irrelevante. Os vetores V7 e V8 são vetores nulos, e por isso não foram apresentados na figura.
Controles
Existem basicamente dois controles que operam nesse modelo da microturbina sendo que não há nenhuma troca de informações entre eles. Um primeiro controle é responsável por ajustar a potência gerada pela turbina para que a demanda da carga seja atendida e que a bateria se mantenha devidamente carregada. Pode-se dizer que a área de atuação dele vai da turbina até o elo CC.
O segundo controle atua do elo CC até a carga e é responsável pela geração da tensão de saída da microturbina. Ele transforma a energia presente no elo CC em uma forma compatível com a rede através do comando da comutação das chaves do inversor.
Controle da Potência de Geração
No nosso modelo de bateria, a capacidade de carga da mesma é representada por um capacitor. Sendo assim, pode-se considerar que a carga da bateria varia conforme o quadrado da tensão (E=0,5.C.V2; onde E é a energia armazenada no capacitor, C é a sua capacitância e V é a tensão sobre os seus terminais). Essa característica tensão x energia armazenada é utilizada para se fazer o controle da potência de geração.
A potência produzida pela turbina é ajustada através de um controle que visa manter o nível de tensão no elo CC em um valor que representa a condição de carga ideal das baterias (condição de carga na qual elas são capazes de suprir os maiores aumentos e diminuições de carga). Quando, por exemplo, um aumento de carga se apresenta, ele é primeiramente suprido pelas baterias localizadas no elo CC. Isso faz com que as baterias se descarreguem, ocasionando uma diminuição da sua tensão terminal. A tensão terminal é comparada com uma tensão de referência, resultando assim um erro. Esse erro alimenta um controlador PI que determina que a turbina aumente a sua geração de potência até que o nível de tensão no elo CC se iguale ao da referência, condição na qual a bateria se apresentará novamente carregada..
O esquema da figura 7 apresenta esse método de controle da turbina através da manutenção do nível de tensão no elo CC. A turbina, é representada por um sistema de primeira ordem com uma saída limitada ao seu valor máximo de geração de potência (blocos "característica da microturbina" e "Pot Max da turbina"). Na referência (CERTS, 2001) apresentam-se alguns resultados de testes realizados com dois modelos de microturbinas. Esses resultados confirmam a utilização de um sistema de primeira ordem como uma boa aproximação para representar a dinâmica da microturbina e foram utilizados para a obtenção da constante de tempo da turbina.
O torque máximo que pode ser aplicado no eixo de um gerador síncrono, qualquer que seja sua velocidade, é constante e de valor descrito pela equação (5) (Ryan, 2000). Deste modo, coloca-se um limitador de torque na saída do controlador para evitar que o GIP saia de sincronismo. Na prática é inviável fazer a limitação do valor do torque desse modo. Uma melhor opção seria controlar a potência gerada pela microturbina (P), não permitindo que a relação P/ωm ultrapasse o limite de torque do GIP.
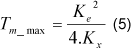
Controle do Inversor
O controle apresentado a seguir, foi em grande parte baseado nas referências (Lasseter, 2000) e (Chandorkar, 1993). Primeiramente será tratada a estratégia de controle quando a microturbina estiver operando em conexão com a rede. Posteriormente, a situação de operação sem a conexão com a rede será discutida.
Controle do Inversor em conexão com a rede
O fluxo de potência ativa e reativa que deixa a microturbina é obtido através das medidas de tensão feitas sobre um indutor instalado na saída do inversor, conforme pode ser visto na figura 8. A indutância desse indutor, que também funciona como um filtro, deve ser devidamente escolhido para que se consiga a potência ativa (P) e reativa (Q) desejadas sem que sejam necessárias grandes tensões no inversor. Um método para se determinar o valor dessa indutância é descrito na referência (CERTS, 2000).
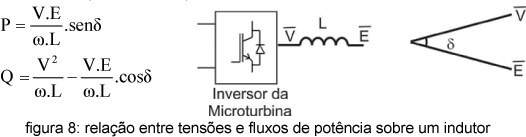
Percebe-se então que com a ajuda de um indutor conectado à saída do inversor, pode-se controlar a potência ativa e reativa produzida pela microturbina através do controle das variáveis |V| e δ, ou seja, através do vetor tensão de saída imagemaqui. Contudo, a descontinuidade da tensão V, gerada pela comutação das chaves do inversor, torna bem complicado o controle direto dessas variáveis (|V| e δ). Por isso, são definidos os vetores de fluxo do inversor Ψv e Ψe, que são a integral no tempo da tensão de saída após o inversor (Ψv) e após o indutor (Ψe), e o ângulo δp, que é o ângulo formado entre esses dois vetores. As equações (6) à (9) determinam a magnitude e a fase do vetor imagemaqui (imagemaqui é obtido de modo análogo) e a equação (10) determina o ângulo δp. Os módulos e os ângulos de imagemaqui e imagemaqui determinam a potência ativa e reativa produzida pelo inversor quando substituídas nas equações (11) e (12) (Chandorkar, 1993).
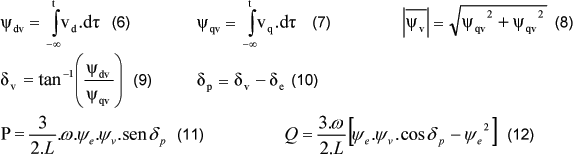
Verifica-se então que o controle de P e Q pode ser feito através do controle de δp e Ψv respectivamente. Esse controle através do vetor de fluxo tem demonstrado um bom desempenho tanto em regime permanente como em transitórios. Ele também fornece um meio mais adequado para se definir o ângulo de potência, já que as constantes mudanças do vetor de tensão da saída do inversor não produzem nenhuma descontinuidade no vetor de fluxo (Chandorkar, 1993).
Para que se ajuste δp e Ψv, é necessário saber qual é o valor de referência (δpo e Ψvo) que essas variáveis devem ter para que os fluxos de potência (P e Q) que passam pelo inversor sejam iguais aos determinados pelo operador da microturbina. O valor de δpo é obtido através da saída de um regulador PI que é alimentado pela diferença entre a fluxo de potencia ativa desejado e o fluxo de potencia ativa medido. O valor de Ψvo é obtido de modo análogo através de um regulador PI alimentado pela diferença do fluxo de potência reativa desejado e medido.
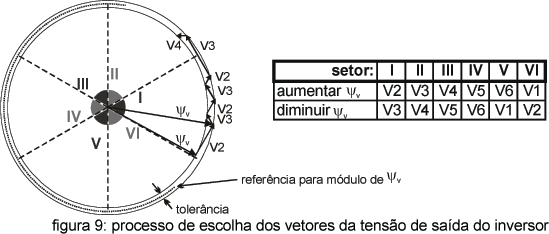
De posse dos valores de referência δpo e Ψvo, o ajuste do valor de δp e Ψv será feito com a escolha do correto vetor de tensão na saída do inversor (ver figura 6), determinada através da tabela presente na figura 9. Essa escolha leva em conta o setor (I, II...VI) em que o vetor de fluxo está localizado e a necessidade de aumentar ou de diminuir δp e Ψv. Sendo assim, tanto δp como Ψv são comparados com valores de referências δpo e Ψvo. Quando a diferença entre δp e Ψv e suas referências ultrapassam uma determinada tolerância um outro vetor de tensão é escolhido, o que ajusta δp e Ψv para valores mais próximos de suas referências. Como se pode perceber trata-se de um tipo de controle com histerese, que mantém as variáveis δp e Ψv sempre próximos de suas referências. É importante salientar que os vetores não nulos (V1...V6) aumentam δp e os vetores nulos V7 e V8 diminuem δp. Analisando a figura 9 pode se entender melhor como é feita a escolha dos vetores para o ajuste do módulo de Ψv.
A figura 10 apresenta o esquema de controle do inversor quando conectado com a rede. Um regulador PI controla os valores de δpo e Ψvo para que, respectivamente, as medidas de P e Q se tornem iguais aos valores de potência ativa e reativa de referência, determinados pelo operador da microturbina. Os valores de Ψv e δv são obtidos através da tensão de saída do inversor e os valores Ψe e δe são obtidos através das tensões medidas após o indutor. Como já descrito no parágrafo anterior, a escolha do vetor de tensão é feita através da comparação entre δp e δpo e entre Ψv e Ψvo.
Controle do inversor sem conexão com a rede
A principal diferença nessa situação é que o inversor não tem a tensão de referência da rede. Portanto, nesse caso o inversor determinará as referências δpo e Ψvo com o intuito de fornecer a tensão de saída do inversor com módulo e freqüência requisitados pelo operador da microturbina.
Sendo assim, os controles de P e Q, que fornecia os valores de δpo e Ψvo, utilizados no item anterior serão substituídos pelos controles de freqüência e tensão.
No caso de termos uma instalação com mais de uma microturbina, é necessário que a carga seja distribuída de maneira apropriada entre elas. Essa divisão de carga tem que se dar automaticamente após uma mudança de carga e não pode ser dependente de canais de comunicação externos. O método utilizado para fazer essa divisão de carga é o mesmo utilizado na operação do sistema elétrico: fazer com que a freqüência da tensão gerada pelas unidades geradoras (microturbinas) varie conforme a potencia ativa que elas produzem (Kundur, 1993). A equação básica desse método é apresentada na equação (12).
ωi = ω0 - mi (Pil - Pi) (12) onde, ωi é a freqüência gerada pelo gerador i, ωo é a freqüência nominal do sistema, Pni é a potência nominal do gerador i e Pi e a potência que está sendo produzida pelo gerador i. mi é a característica freqüência x potência do gerador i e é escolhida proporcionalmente à capacidade do gerador.
A freqüência da tensão gerada pela microturbina (ωi), determinada pela sua condição de carga, será ajustada pelo controle de freqüência. No controle de freqüência, a freqüência ωi é integrada a fim de se obter uma referência (δaco) para o ângulo da tensão de saída da microturbina (δac). A diferença entre δaco e δac alimenta um regulador PI que vai gerar a referência do ângulo de potência δpo. A mudança de δpo vai alterar a potencia gerada P, que está intimamente ligada com a freqüência da tensão gerada.
O controle de tensão, utilizado para ajustar o módulo da tensão gerada pelo indutor, compara o valor de tensão de referência desejado na saída da microturbina com o produto do módulo do vetor de fluxo ΨE pela freqüência da tensão gerada ωi (para uma tensão senoidal Ψ.ω=V). O erro proveniente dessa comparação alimenta um regulador PI que gera a referência do módulo do vetor de fluxo Ψvo. A mudança de Ψvo acarreta numa alteração da potência reativa gerada, que está intimamente ligada com o módulo da tensão gerada.
Os esquemas dos controles de freqüência e tensão podem ser visualizados na figura 11.
SImulação
Para que a simulação fosse menos demorada, a constante de tempo da turbina foi considerada igual a 1 seg. Para se avaliar o comportamento de uma microturbina com constante de tempo diferente é só multiplicar a escala de tempo pelo valor da constante em segundos. A capacidade da bateria foi especificada também considerando a constante de tempo da turbina igual a 1 seg.
As figuras 12, 13 e 14 referem-se a um degrau de carga de 1kW para 2kW nos terminais da microturbina quando não conectada a rede. Na figura 12 é apresentado a variação da potência produzida pelo sistema gerador-retificador, pela bateria e pelo inversor.
A figura 13 apresenta a tensão de saída do inversor e da microturbina. A tensão de saída da microturbina tem conteúdo harmônico de aproximadamente THD=1,8%.
A figura 14 demonstra como a tensão no elo CC se comporta com essa variação de carga.
REFERÊNCIAS
[1] Robert Lasseter; Dynamic Models for Micro-Turbine and Fuel Cells; IEEE Power Engineering Society 2001 Summer Meeting; 2001.
[2] Y. Zhu, K. Tomsovic; Development of models for analyzing the load-following performance of microturbines and fuel cells; Electric Power Systems Research 62; 2002.
[3] E. Cengelci, P. Enjeti; Modular PM Generator/Converter Topologies, Suitable for Utility Interface of Wind/Micro Turbine and Flywheel Type Electromechanical Energy Conversion Systems; Industry Applications Conference, 2000. Conference Record of the 2000 IEEE; Volume 4 ; October; 2000.
[4] Chee-Mun Ong; Dynamic Simulations of Electric Machinery : Using MATLAB/SIMULINK; Pearson Education; September; 1997.
[5] M. S. Illindala, G. Venkataramanan; Battery Energy Storage for Stand-Alone Micro-Source Distributed Generation Systems; 6th IASTED Intl. Conf. On Power and Energy Systems; May, 2002.
[6] Consortium for Electric Reliability Technology Solutions (CERTS); Behavior of Capstone and Honeywell Microturbine Generators during Load Changes; July; 2001.
[7] M. J. Ryan, R. D. Lorenz; A Novel Controls-Oriented of a PM Generator With Diode Bridge Output; 6th EPE Conf. Record; Trondheim, Norway; September; 1997.
[8] Robert Lasseter; Providing Premium Power Through Distributed Resources; Proceedings of the 33rd Hawai Internatil Conference on System Sciences; 2000
[9] Mukul C. Chandorkar; Deepakraj M. Divan; Rambabu Adapa; Control of parallel connected inverters in standalone AC supply systems; IEEE Transactions on Industry Applications; Volume 29; Issue 1; Jan-Feb; 1993.
[10] Consortium for Electric Reliability Technology Solutions (CERTS);Scenarios for Distributed Applications with Steasy State and Dynamic odels of Loads and Micro-Sources; April; 2000.
[11] Prabha Kundur; Power System Stability and Control; McGraw-Hill; January; 1994.










 How to cite this paper
How to cite this paper