An. 2. Seminário Música, Ciência e Tecnologia 2005
Espaços homogêneos de parâmetros para controle de efeitos musicais
Nicolau Werneck; Furio Damiani
Departamento de Semicondutores, Instrumentação e Fotônica—FEEC —UNICAMP. nwerneck@cefala.org, furio@fee.unicamp.br
RESUMO
No estudo de timbres encontram-se muitas funções dependentes de vários parâmetros, como análises quantitativas ou qualitativas de sistemas de síntese ou processamento sonoro. Os espaços constituídos pelos parâmetros costumam ser heterogêneos, no sentido de que deslocamentos de uma mesma distância no espaço podem causar mudanças de magnitudes diferentes nas funções. Neste trabalho criamos um mapeamento a partir de dois parâmetros de um modelo de overdrive, para um espaço mais homogêneo. Um mapeamento destes é útil na realizaç ão de testes psicoacústicos, possibilitando a obtenç ão de conjuntos de amostras varrendo de forma eficiente as possibilidades de timbres oferecidas pelo sistema em estudo.
Palavras-chave: Síntese Sonora , Estudos de Timbres
ABSTRACT
In the study of timbre, it's usual to find functions that depend on many parameters, like quantitative or qualitative analysis of systems for acoustic synthesys or analysis. The spaces constituted by these parameters are often heterogeneous, meaning that displacements of a same distance in the space can cause changes of different magnitudes in the functions. In this work we created a mapping from the two parameters of an overdrive model to a more homogeneous space. A mapping like this is useful in the realization of psychoacoustic tests, enabling the researcher to obtain sets of samples sweeping in an efficient way the timbre possibilities of the system in study.
Key-words: Sound Synthesis , Timbre
1. Introdução
Músicos se valem de diferentes sistemas para criar timbres musicais. Cada sistema possui um número de parâmetros de controle. Neste trabalho investigamos, para um certo sistema, uma maneira de criar um conjunto alternativo de parâmetros que sejam homogêneos, no sentido de que variações de igual magnitude nos parâmetros impliquem em variações timbrísticas igualmente intensas [McAdams1995].
O uso de escalas exponenciais no controle da potência de amplificadores de áudio e em teclados musicais são bons exemplos desta idéia de homogeneização. Ela também está relacionada com codificadores de maximizaç ão de entropia, como a lei-m para voz.
Neste trabalho estudamos um modelo para o efeito de overdrive, muito utilizado em guitarras elétricas nos estilos musicais rock e blues. Um dos motivos para a escolha deste efeito é que não há uma boa compreensão de quais características físicas do sinal distorcido causam as diferenças de timbre, e existe muita polêmica a respeito das diferenças entre os mecanismos de produção de overdrive.
Apesar de estarmos interessados em desenvolver técnicas para o projeto de sistemas de overdrive musical, o método para homogeneização de parâmetros apresentado aqui pode ser aplicado em qualquer tipo de sistema, e a princípio com qualquer número de parâmetros.
1.1 Modelo utilizado
O overdrive ocorre naturalmente em diversos tipos de sistema. Em geral ele surge quando o sinal extrapola uma faixa de operaç ão linear. Existem diversas funções não-lineares que produzem overdrive. Nosso modelo se baseia numa funç ão de simetria ímpar, composta por segmentos de reta, representada na figura 1. Os dois parâmetros de controle desse modelo são o limiar de nível de sinal antes que comece a saturação, e a intensidade com que o sinal é cortado. No caso extremo, uma senóide na entrada gera uma onda quadrada.
Como o modelo foi implementado de forma digital, a função foi definida para que a maior intensidade de sinal (± 32767 para 16 bits) fosse mapeada para o mesmo valor na saída, evitando qualquer tipo de overflow no processamento. Os sinais foram processados em ponto-flutuante, com as intensidades máximas mapeadas para ±1.0. A figura 2 mostra a parte positiva da função para diferentes pares de parâmetros. Os parâmetros de controle são exatamente as coordenadas do ponto de encontro dos dois segmentos de reta.
Após a aplicação da função, o sinal de saída foi sempre normalizado para ficar com a mesma intensidade RMS do sinal de entrada. Isto é necessário porque pela própria definição usual de timbre, queremos discriminar os sinais por algo além de suas potências [Fletcher1934]. Em nosso modelo, esta normalização sempre implica em uma atenuação do sinal de saída, impossibilitando novamente qualquer tipo de overflow.
Esta função de overdrive com segmentos de reta pode ser implementada em circuitos com amplificadores operacionais, e portanto não está distante da realidade, apesar de ser simples. Modelos mais complexos a serem estudados devem ser capazes de criar funções assimétricas e suaves, como ocorre em cultuados equipamentos antigos [Sedra].
2. Obtenção dos dados
Os dados que estudamos são geralmente medições de limiares de diferença minimamente perceptivel, ou just noticeable difference [wikiJND]. Este conceito pode ser aplicado em três diferentes níveis em nosso modelo: os níveis físico (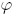 ), psico-físico (
), psico-físico (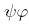 ) e puramente psicológico (
) e puramente psicológico (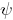 ). Em cada nível avalia-se o seguinte:
). Em cada nível avalia-se o seguinte:
• 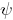 : Se os efeitos causados por dois diferentes pares de parâmetros atendem a uma mesma necessidade musical, ou se são adequados a um certo contexto.
: Se os efeitos causados por dois diferentes pares de parâmetros atendem a uma mesma necessidade musical, ou se são adequados a um certo contexto.
• 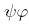 : Se os diferentes efeitos são perceptualmente idênticos.
: Se os diferentes efeitos são perceptualmente idênticos.
• 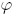 : Se os diferentes efeitos obedecem a algum critério de seleç ão baseado em medidas estatísticas de variáveis físicas.
: Se os diferentes efeitos obedecem a algum critério de seleç ão baseado em medidas estatísticas de variáveis físicas.
Em nosso estudo trabalhamos apenas no nível físico, com o objetivo de nos preparar para a pesquisa nos níveis mais abstratos. O critério estabelecido para substituir a jnd foi o seguinte: Dadas duas amostras normalizadas, calcula-se a diferença entre esses dois sinais. Se a potência média desta diferença for menor do que um certo limiar, considera-se que as amostras são idênticas.
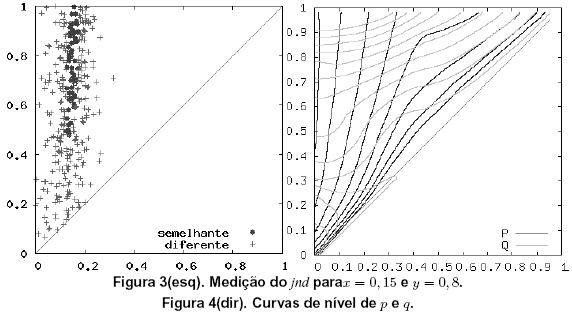
Para medir-se a jnd de um determinado par de parâmetros, é preciso comparar o sinal relativo a estes parâmetros com os sinais gerados por outros pares de parâmetros. Realizando-se esta comparaç ão para várias amostras e uma mesma referência, encontramos algo como a figura 3.
3. Procedimentos
As referências para as medições de jnd foram pontos numa grade regular de 51 por 51 valores, cobrindo todo o intervalo de 0 a 1 em cada dimensão, e com y > x. Os pares de parâmetros comparados com cada referência escolhida foram amostrados de forma aleatória e adaptativa, em que a função de densidade de probabilidade se aproxima aos poucos a uma amostragem em que metade dos pontos caem dentro da elipse de amostras similares, de maneira uniforme, e metade cai fora, com densidade decaindo com a distância à elipse. Este procedimento foi desenvolvido para experimentos psico-acústicos.
De cada nuvem obtivemos dois vetores, como numa PCA [wikiPCA]. Estes vetores são ortogonais, e modelam a região de similaridade como uma elipse.
Em nosso caso, simplesmente supusemos que as direções maiores eram vetores dados por (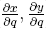 ), e que os vetores menores constituíam as derivadas em relação a p. Desta forma, a variável p se tornou a maior responsável pela variedade de timbres do modelo, já que variações nela criarão menores trajetórias no espaço (x, y).
), e que os vetores menores constituíam as derivadas em relação a p. Desta forma, a variável p se tornou a maior responsável pela variedade de timbres do modelo, já que variações nela criarão menores trajetórias no espaço (x, y).
Para determinar o mapeamento, é necessário tomar cada um destes valores de derivadas parciais, e montar uma matriz jacobiana que, invertida, nos fornece os valores das derivadas parciais de p e q em relação a x e y. Estas derivadas definem por sua vez dois campos que se supõe serem gradientes das funções que dão p e q a partir de (x, y).
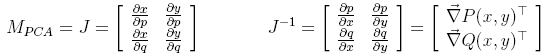
Integramos estes campos por diferenças finitas, montando um sistema esparso de centenas de variáveis. O sistema foi resolvido pelo método GMRES.
4. Resultados
A figura 4 mostra as curvas de nível de p e q em funç ão de (x, y). A figura mostra exatamente qual é o aspecto de uma grade em (p, q) quando projetada em (x, y). Entretanto, a amostragem de valores da função p foi feita de forma exponencial, em potências de 2. Isto significa que se fosse feita uma amostragem a intervalos iguais haveria muito mais curvas relativas a níveis de p na região mais próxima de x = 0.
5. Conclusões
As curvas de nível deveriam ser perfeitamente ortogonais, mas isto não ocorreu porque os campos obtidos não eram integráveis. é preciso estudar como a imposiç ão da integrabilidade sobre os campos pode ser explorada para obter-se diferentes resultados.
O método desenvolvido neste trabalho funcionou bem, justificando seu uso na escolha de conjuntos reduzidos de referências para uso em experimentos psico-acústicos. Análises mais aprofundadas poderão justificar o uso de alguma técnica similar na criação de espaços timbrísticos em que eixos são funções não-lineares de parâmetros físicos.
6. Agradecimentos
Agradecemos ao CEFALA da UFMG, onde parte do trabalho foi concebido e realizado.
Este trabalho foi financiado pela CAPES.
Referências
[McAdams1995] S. McAdams,W.Winsberg, S. Donnadieu, G. De Soete and J. Krimphoff, “Perceptual scaling of synthesized musica timbres: Common dimensions, specificities, and latent subject classes.” Psychological Research, 58, pp. 177–192, 1995.
[Fletcher1934] H. Fletcher, “Loudness, pitch and the timbre of musical tones and their relation to the intensity, the frequency and the over-tone structure.” Journal of the Acoustical Society of America 6, pp. 59–69. 1934.
[Sedra] Sedra, Smith, “Microelectronic Circuits”, Oxford University Press, 5th ed.
[wikiJND] Wikipedia, www.wikipedia.org, artigo just noticeable difference
[wikiPCA] Wikipedia, www.wikipedia.org, artigo principal component analisys










 How to cite this paper
How to cite this paper