An. 2. Seminário Música, Ciência e Tecnologia 2005
Sistemas de afinação: um apanhado histórico
Alexandre Torres Porres; Jônatas Manzolli
Departamento de Música - Instituto de Artes. Núcleo Interdisciplinar de Comunicação Sonora – Universidade Estadual de Campinas (UNICAMP). 13.081-970 – Campinas – SP – Brasil. porres@nics.unicamp.br, jonatas@nics.unicamp.br
RESUMO
Este artigo descreve o desenvolvimento da afinação pitagórica aos temperamentos, também comentando sobre os sistemas de divisão múltipla. A discussão sobre a evolução destes sistemas pretende abordar o panorama mais recente, onde se incluem as pesquisas microtonais do século XX.
Palavras-chave: Sistemas de Afinação , Afinação Pitagórica , Temperamentos , Acústica de Instrumentos Musicais
ABSTRACT
This paper describes the development from pythagorean tuning to the temperaments, also describing the multiple division systems. The discussion about the evolution of such systems intends to approach the more recent panorama, where the microtonal researches from the 20th century are included.
Key-words: Tuning Systems , Pythagorean System , Tempered Tuning , Acoustics of Musical Instruments
1. Introdução
Este artigo apresenta uma proposta de trajetória histórica para a evolução dos Sistemas de Afinação divida em três seções. Em Afinação Pitagórica e Temperamentos descreve-se como o conceito de Afinação Pitagórica esteve presente na Idade Média até o surgimento do temperamento durante o Barraco. Segue a apresentação de alguns sistemas temperados de mais de 12 divisões por oitava, denominados de Divisões Múltiplas. Finalmente, faz-se uma descrição do desenvolvimento de tais sistemas no contexto do Século XX.
A trajetória aqui apresentada é vinculada aos trabalhos de Barbour (1951) e Partch (1949) na qual se fixa uma relação entre a Afinação Justa e o Temperamento sob a ótica do que é denominado de Limite de um Sistema de Afinação. A hipótese aqui descrit\a é vinculada ao trabalho de Partch (1949), onde se postula que há uma relação de complexidade entre os sistemas de afinação, os seus Limites e a avaliação de consonância1. Nas próximas seções há um conjunto de Tabelas relacionadas a cada período histórico e pode-se notar para cada Sistema descrito qual o Limite no qual o mesmo está inserido. Assim, tomamos como ponto de partida os seguintes conceitos:
· Intervalos justos são representados por proporções de números inteiros. Ex: [2:1] (oitava), [3:2] (quinta). Intervalos temperados são representados por proporções de números irracionais. Ex: [2½:1] = 1,4142... (trítono temperado). A Afinação Justa possui apenas intervalos justos, enquanto que o Temperamento, além de intervalos temperados, pode conter intervalos justos.
· Limite de um sistema de Afinação: O Limite de um sistema de afinação justa é dado pelo fator primo de maior valor. Ex: [45:32] = [5*32:25] – Limite-5, [21:20] = [7*3:5x22] – Limite-7.
· Os valores nas Tabelas são dados em suas proporções numéricas e descritos em cents 2.
2. Afinação Pitagórica e Temperamentos
2.1. Da Idade Média ao Renascimento (Afinações Justas)
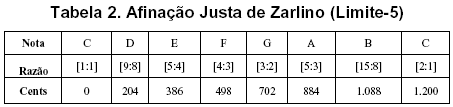
O padrão vigente na Idade Média foi a Afinação Pitagórica, baseada em intervalos justos de quintas [3:2]. Uma vez que todas as proporções possuem apenas os fatores 2 e 3 (tabela 1), esta afinação está no Limite-3. A terça maior Pitagórica, que é formada por uma sucessão de quintas (proporção de [81:64]), esta relacionada a termos mais altos da Série Harmônica (SH) e, portanto, menos consonante que a terça maior representada pela proporção [5:4] (Limite-5, relação entre o quarto e o quinto termo da SH). Quando a entonação de terças no limite-5 começou a ser utilizada, no fim da Idade Média, a terça maior deixou de ser considerada instável.
Ao incluir o limite-5, Logo, na Escala de Zarlino (tabela 2), a sexta maior [5:3] não forma o intervalo de uma quinta com a segunda maior [9:8] e sim o intervalo dissonante de [40:27]. Quando esta Escala é utilizada na tonalidade de Ré temos um problema de entonação com a quinta (a nota Lá). Este problema de limitação de modulação gerou a necessidade de se construir Sistemas Temperados, elaborados, para encontrar boas soluções e aproximar afinações justas no limite-5. O objetivo foi obter, com um mesmo intervalo temperado, uma aproximação para um intervalo justo no Limite-3 e no Limite-5.
2.2. Do Barroco ao Século XX (Temperamentos)
No período barroco temos os “Temperamentos Mesotônicos”, que possibilitaram modulações restritas. Os “Bem-Temperamentos” do século XVIII disponibilizaram o uso de todas as tonalidades, porém, por serem desiguais, Cada tonalidade possuía uma distribuição própria de intervalos. Qual propriedade fazia com que houvesse uma variação do grau de consonância e dissonância dos intervalos de cada tonalidade, sendo que as mais próximas de Dó Maior tinham sonoridades mais consonantes. Ao final do século XIX, os temperamentos elaborados se tornaram cada vez menos desiguais por causa da prática de modulações para tonalidades cada vez mais distantes. Isso culminou na padronização do temperamento que possibilita a modulação para todos os tons, sendo que todos possuem a mesma distribuição intervalar (i.e. o Temperamento Igual).
Nota-se que a necessidade de modulação para diferentes tonalidades foi mais importante que a necessidade de aproximação do limite-5, uma vez que a terça maior temperada (400 cents) não é uma boa aproximação do intervalo de [5:4] (386 cents). Ironicamente, o temperamento igual tem seus intervalos mais próximos do Limite-3 (Afinação Pitagórica), pois a diferença entre a quinta pura e a quinta temperada é de apenas 2 cents.
3. Divisões Múltiplas
As divisões múltiplas da oitava surgem como uma nova alternativa para os problemas de entonação, apresentamos na seção anterior, pois ao incluir mais intervalos por oitava, eventualmente haverá mais espaço para aproximar os limites de afinação.
3.1. Divisão Múltipla da Oitava em 19 Tons
Zarlino (1517-1590) e Salinas (1513-1590) construíram instrumentos de teclado com 19 divisões da oitava, ambos afinados em um temperamento mesotônico expandido (2/7 de coma3 e 1/3 de coma respectivamente, sendo que o último resultava em uma divisão quase igual). Elaborados como aproximações do Limite-5, estes sistemas ampliam a possibilidade de modulação dos temperamentos mesotônicos originais.
3.2. Divisão Múltipla da Oitava em 31 Tons
Nicolas Vicentino (1511-1576) construiu o “Archicembalo”, com seis teclados e 31 tons por oitava. Afinado também em um temperamento mesotônico (1/4 de coma), foi da mesma maneira elaborado como uma melhor aproximação do Limite-5. Um século depois, o holandês Cristiaan Huygens (1629-1695) demonstrou que o temperamento de divisão da oitava em 31 partes iguais continha intervalos muito similares ao temperamento mesotônico de 1/4 de coma. Huygens também apontou como este temperamento igual possui uma boa aproximação de intervalos no limite-7.
3.3. Divisão Múltipla da Oitava em 53 Tons
Mersenne (1588-1648) descreve o sistema de divisão da oitava em 53 tons proposta pelos autores gregos antigos, que é literalmente uma escala de comas pitagóricas4, formadas por sucessões de quintas [3:2], portanto trata-se de uma afinação justa no limite-3, porém, pelo grande número de intervalos, há uma boa aproximação do limite-5. Esta descrição serviu de base para R. H. M. Bonsaquete Tanaka Shohé, que no fim do século XIX construíram instrumentos afinados no temperamento igual de 53 tons por oitava, elaborados como uma boa aproximação do limite-5, porém com problemas práticos de execução.
4. Panorama do Século XX
4.1. Além do Limite-5
Apesar da aproximação do limite-7 com a divisão igual da oitava em 31 tons, descrito por Huygens no século XVII, o uso de um sistema de afinação justa superior ao limite-5 (ou aproximação por temperamento) não foi adotado por nenhum compositor ocidental até o século XX, porém Giuseppe Tartini (1692-1770) desenvolveu uma notação especial para intervalos de [7:4] (intervalo justo de sétima menor).
4.1.1. Harry Partch
O compositor Americano Harry Partch (1901-1974) construiu diversos instrumentos para o seu sistema de afinação justa no Limite-11, com 43 tons por oitava. As tonalidades completas de Partch possuem apenas 06 notas (tabela 3).
4.1.2. Adriaan Fokker
O holandês Adriaan Fokker (1887-1972), baseado na descrição de Huygens, construiu um órgão no temperamento igual de 31 tons por oitava, usado agora como uma aproximação do Limite-7.
4.2. Divisões do Tom
No século XX surgiram subdivisões do temperamento igual de 12 notas por oitava como terços, quartos, quintos e sextos de tom. Porém, assim como o temperamento igual de 12 notas, estas subdivisões não são boas aproximações do limite-5. Alois Hába (1893-1973), um dos maiores nomes da música microtonal do século XX, compôs uma vasta obra usando sistemas microtonais de subdivisão do tom, sendo a maioria em quartos de tom.
Mais recentemente, compositores como Gerard Grisey fizeram uso destas subdivisões na Música Espectral com o intuito de criar uma aproximação do contínuo de freqüências. Neste caso, o objetivo não foi, necessariamente, aproximar os limites dos sistemas de afinação, mas sim gerar tanto relações inarmônicas quanto harmônicas e encontrar novas sonoridades para combinação de paletas instrumentais. Com recursos microtonais busca-se fundir as relações de harmonia e timbre e, nessa abordagem, não se adota um sistema de afinação fixo.
5. Conclusões
Até o século XX, na música ocidental, os sistemas de afinação justa evoluíram de sistemas no limite-3 (baseados em intervalos justos de quintas) para sistemas no limite-5 (baseados em intervalos justos de quintas e terças), o que gerou a necessidade do temperamento e divisões múltiplas. No século XX, alguns sistemas de afinação alternativos buscaram utilizar limites superiores ao limite-5, como o sistema de Harry Partch. Já Fokker utilizou um temperamento igual como aproximação do limite-7, descrito por Huygens no século XVII. Divisões do tom, como quartos de tom e sextos de tom, partem do princípio de expansão do sistema temperado que divide a oitava em 12 partes iguais, e não de aproximações de limites. A música espectral se vale do uso de microtons para gerar texturas complexas e dinâmicas, sem as mesmas estarem vinculadas a um sistema de afinação fixo.
O escopo deste artigo faz parte de um projeto de mestrado no qual o autor deverá explorar os elementos aqui descritos no desenvolvimento de um sistema de composição próprio.
Agradecimentos
Este trabalho tem o apoio da FAPESP através de projeto de mestrado e apoio do CNPq através de bolsa de produtividade em pesquisa.
Referências
Beer, Anton de. (1965) “The Development of 31-tone Music”, http://www.xs4all.nl/~huygensf/doc/beerart.html, acesso em outubro de 2005.
Barbour, J. Murray. Tuning and Temperament – A Historical Survey, Michigan State Collage Press, 1951.
Haba, Alois. Nuevo Tratado de Armonía, Madrid, Real Musical S.A., 1984.
Helmholtz, Hermann. On the Sensations of tone. New York, Dover Publications, 1954.
Partch, Harry. Genesis of a Music, University of Wisconsin Press, 1949.
Wolf, Daniel James. "Alternative tunings, alternative tonalities", Contemporary Music Review vol. 22 no. 1-2, March-June 2003, pp. 3-14.
21 Neste trabalho o conceito de consonância e dissonância é atribuido aos termos da Série Harmônica de forma que quanto maior forem os termos numéricos de que descrevem um intervalo, o mesmo será considerado mais dissonante.
2 Um Cent equivale a um centésimo do semitom temperado, e é usado como medida de intervalos por nos dar uma relação precisa ao sistema padrão atual – o temperamento que divide a oitava em 12 partes iguais.
3 Quando o tipo de coma não é mencionado, como neste caso, normalmente trata-se da coma sintônica, que é a diferença entre a terça maior pitagórica [81:64] e a terça maior justa [5:4].
4 A Coma pitagórica é a diferença entre 7 oitavas (2:1) e 12 quintas (3:2).










 How to cite this paper
How to cite this paper